Problems
A game of ’Battleships’ has a fleet consisting of one \(1\times 4\) square, two \(1\times 3\) squares, three \(1\times 2\) squares, and four \(1\times 1\) squares. It is easy to distribute the fleet of ships on a \(10\times 10\) board, see the example below. What is the smallest square board on which this fleet can be placed? Note that by the rules of the game, no two ships can be placed on horizontally, vertically, or diagonally adjacent squares.
The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.The sequence \(a_1, a_2, \dots\) is such that \(a_1 \in (1,2)\) and \(a_{k + 1} = a_k + \frac{k}{a_k}\) for any positive integer \(k\). Prove that it cannot contain more than one pair of terms with an integer sum.
Prove that if the expression
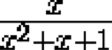
takes a rational value, then the expression
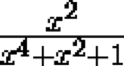
also takes on a rational value.
What is the smallest number of ‘L’ shaped ‘corners’ out of 3 squares that can be marked on an \(8\times 8\) square grid, so that no more ’corners’ would fit?
An airline flew exactly 10 flights each day over the course of 92 days. Each day, each plane flew no more than one flight. It is known that for any two days in this period there will be exactly one plane which flew on both those days. Prove that there is a plane that flew every day in this period.
10 children, including Billy, attended Billy’s birthday party. It turns out that any two children picked from those at the party share a grandfather. Prove that 7 of the children share a grandfather.
Find \(x^3 +y^3\) if \(x+y=5\) and \(x+y+x^2 y +xy^2 =24\).
On the \(xy\)-plane shown below is the graph of the function \(y=ax^2 +c\). At which points does the graph of the function \(y=cx+a\) intersect the \(x\) and \(y\) axes?
Find the largest natural number \(n\) which satisfies \(n^{200} <5^{300}\).
Does there exist a natural number which, when divided by the sum of its digits, gives a quotient and remainder both equal to the number 2011?