Problems
Decipher the quote from "Alice in Wonderland" from the following
matrix:
\[\begin{array}{@{}*{26}{c}@{}}
Y&q&o&l&u&e&c&d&a&i&n \\
w&a&r&l&a&w&e&a&t&y&k \\
s&n&t&c&a&e&k&c&e&a&m \\
t&o&d&r&w&e&a&t&a&h&r \\
a&c&n&t&n&e&o&d&t&r&h \\
n&i&d&n&l&g&m&e&x&s&z
\end{array}\]
Decipher the following quote from Alice in Wonderland:
Lw zrxog eh vr qlfh li vrphwklqj pdgh vhqvh iru d fkdqjh.
The same letters correspond to the same in the phrase, different letters
correspond to different. We know that no original letters stayed in
place, meaning that in places of e,r,h there was surely something
else.
Elon is studying the Twitter server. Inside the software he found two integer variables \(a\) and \(b\) which change their values when special search queries “RED”, “GREEN”, and “BLUE” are processed. More precisely the pair \((a, b)\) changes into \((a + 18b, 18a - b)\) when processing the query “RED”, to \((17a + 6b, -6a + 17b)\) when processing “GREEN”, and to \((-10a - 15b, 15a - 10b)\) when processing “BLUE”. When any of \(a\) or \(b\) reaches a multiple of \(324\), it resets to \(0\). If \((a, b) = (0, 0)\) the server crashes. On the server startup, the variables \((a, b)\) are set to \((20, 20)\). Prove that the server will never crash with these initial values, regardless of the search queries processed.
After mastering the Caesar shift cypher one may wonder how to generalize it. One possible way is to use Affine cypher. The difference between these two methods can be described as follows:
In case of Caesar cypher we took a letter with position \(n\) from \(1\) to \(26\) and added to its position a number \(d\) obtaining the number \(n+d\), then we compute its residue modulo \(26\).
In case of affine cypher we take a letter with position \(n\) and consider a number \(nx + d\) modulo \(26\).
To decipher such code we need to know values \(x\) and \(d\), then if we have a letter in the code with position \(m\), we can find \(n\) as \(n= (m-d)x^{-1}\) modulo \(26\). Here we have to explain what is \(x^{-1}\): for a number \(x < 26\) we are looking for such a number \(y\), that \(26\) divides \(xy-1\).
Does there always exist a number \(x^{-1}\) modulo \(26\) for any \(x\)?
Using data \(x=3\), \(d=8\) encrypt the word "SOLUTION".
On the grid paper, Theresa drew a rectangle \(199 \times 991\) with all sides on the grid lines and vertices on intersection of grid lines. How many cells of the grid paper are crossed by a diagonal of this rectangle?
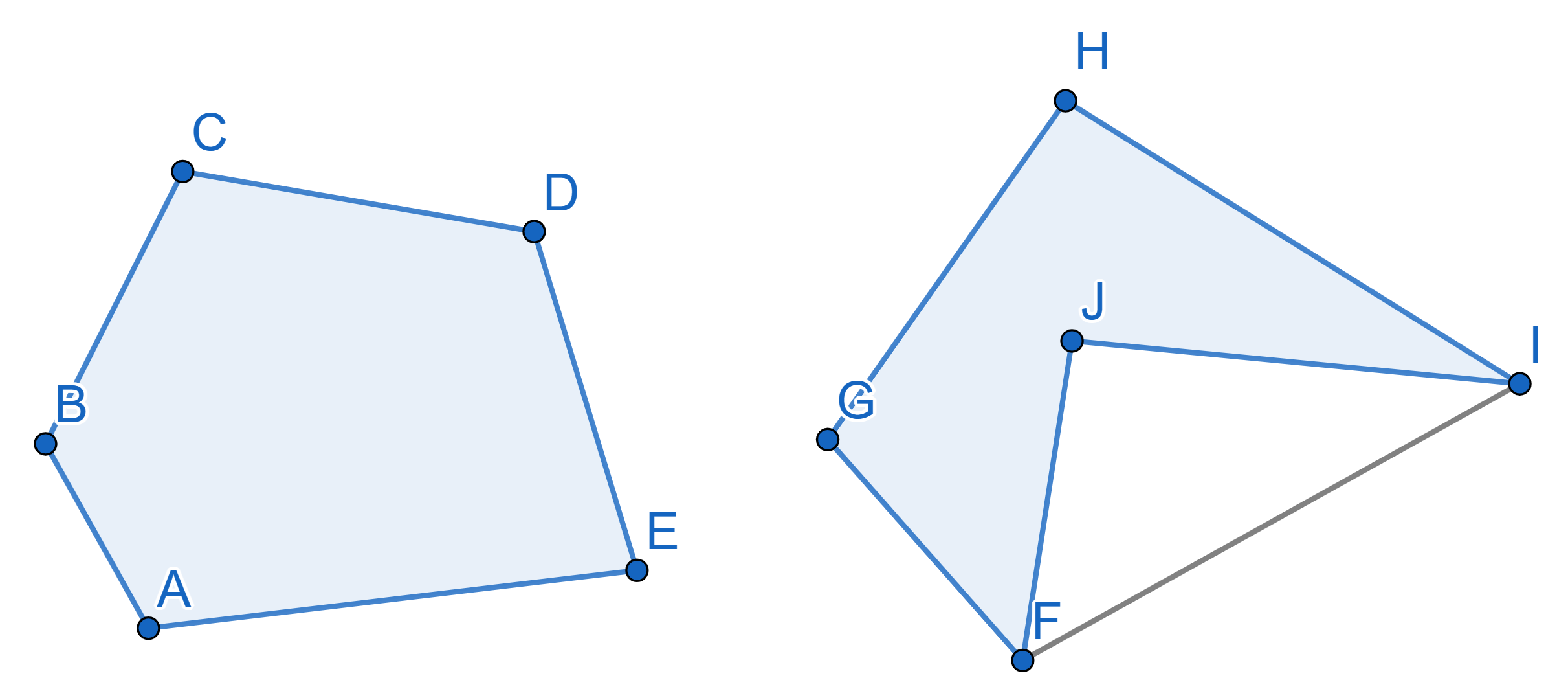
We say that a figure is convex if a segment connecting any two points
lays fully within the figure. On the picture below the pentagon on the
left is convex and the one on the right is not.
Is it possible to draw \(18\) points
inside a convex pentagon so that each of the ten triangles formed by its
sides and diagonals contains equal amount of points?
Cambria was various cuboids from \(1\times 1\times1\) cubes. She initially built one cuboid, then increased its length and width by \(1\) and reduced its height by \(2\). She noticed that she needed the same number of \(1\times 1\times 1\) cubes to build both the original and new cuboids. Show that the number of cubes used for each of the cuboids is divisible by \(3\).
A labyrinth was drawn on a \(5\times
5\) grid square with an outer wall and an exit one cell wide, as
well as with inner walls running along the grid lines. In the picture,
we have hidden all the inner walls from you (We give you several copies
to facilitate drawing) 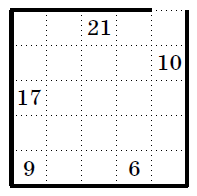


Please draw how the walls were arranged. Keep in mind that the numbers
in the cells represent the smallest number of steps needed to exit the
maze, starting from that cell. A step can be taken to any adjacent cell
vertically or horizontally, but not diagonally (and only if there is no
wall between them, of course).
Is it possible to cut this figure, called "camel"
a) along the grid lines;
b) not necessarily along the grid lines;
into \(3\) parts, which you can use
to build a square?
(We give you several copies to facilitate drawing)



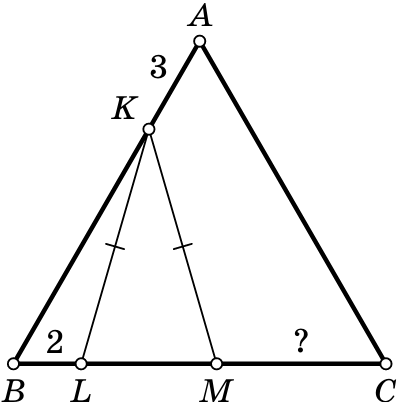
The triangle \(ABC\) is equilateral.
The point \(K\) is chosen on the side
\(AB\) and points \(L\) and \(M\) are on the side \(BC\) in such a way that \(L\) lies on the segment \(BM\). We have the following properties:
\(KL = KM,\) \(BL = 2,\, AK = 3.\) Find the length of
\(CM\).