Problems
Nick has written in some order all the numbers \(1,2,...33\) at the vertices of a regular \(33\)-gon. His little sister Hannah assigned to each side of the \(33\)-gon the number equal to the sum of the numbers at the ends of that side. It turns out that Hannah obtained \(33\) consecutive numbers in certain order. Can you find an arrangement of numbers as written by Nick which lead to this situation?
Jess and Tess are playing a game colouring points on a blank plane. Jess is moving first, she picks a non-colored point on a plane and colours it red. Then Tess makes a move, she picks \(2022\) colourless points on the plane and colours them all green. Jess then moves again, and they take turns. Jess wins if she manages to create a red equilateral triangle on the plane, Tess is trying to prevent that from happening. Will Jess always eventually win?
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetrominos?
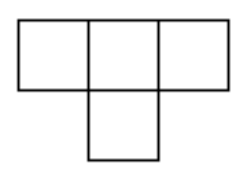
Can you cover a \(10 \times 10\) square with \(1 \times 4\) rectangles?
Two opposite corners were removed from an \(8 \times 8\) chessboard. Is it possible to cover this chessboard with \(1 \times 2\) rectangular blocks?
One unit square of a \(10 \times 10\) square board was removed. Is it possible to cover the rest of it with \(3\)-square \(L\)-shaped blocks?
A \(7 \times 7\) square was tiled using \(1 \times 3\) rectangular blocks in such a way that one of the squares has not been covered. Find all the squares that could be left without being covered.
Can you cover a \(13 \times 13\) square using \(2 \times 2\) and \(3 \times 3\) squares?
Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.
On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.