Problems
On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.
A \((2n - 1) \times (2n - 1)\) board is tiled with pieces of the following possible types:
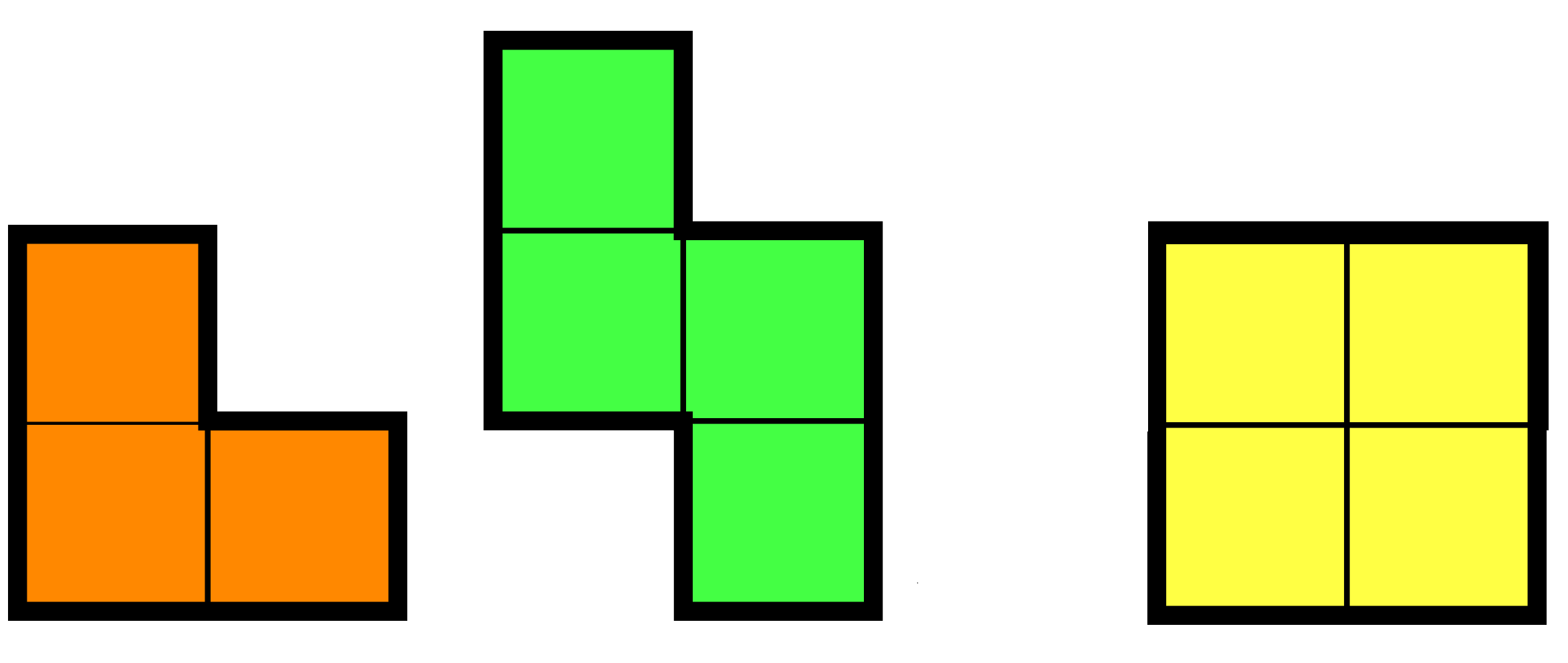
Prove that at least \(4n-1\) of the first type have been used.
In an \(n \times n\) board the squares are painted black or white in some way. Three of the squares in the corners are white and one is black. Show that there is a \(2\times 2\) square with an odd number of white unit squares.
On an \(8\times 8\) board there is a lamp in every square. Initially every lamp is turned off. In a move we choose a lamp and a direction (it can be the vertical direction or the horizontal one) and change the state of that lamp and all its neighbours in that direction. After a certain number of moves, there is exactly one lamp turned on. Find all the possible positions of that lamp.
In an \(5\times 5\) board one corner was removed. Is it possible to cover the remaining board with linear trominos (\(1\times 3\) blocks)?
Convert the binary number \(10011\) into decimal, and convert the decimal number \(28\) into binary. Multiply by \(2\) as binary numbers both \(10011\) and the result of conversion of \(28\) into binary numbers.
The ternary numeral system has only \(3\) digits: \(0,\) \(1\) and \(2\). Therefore the number \(3\) is written in ternary as \(10\). Write down the numbers \(23\) and \(156\) in ternary and add them as ternary.
Write down the first fifteen numbers in binary system.
Given a natural number \(n\) you are allowed to perform two operations: "double up", namely get \(2n\) from \(n\), and "increase by \(1\)", i.e. to get \(n+1\) from \(n\). Find the smallest amount of operations one needs to perform to get the number \(n\) from \(1\).
Alice the fox and Basilio the cat have grown \(20\) counterfeit bills on a money tree and now write seven-digit numbers on them. Each bill has \(7\) empty cells for numbers. Basilio calls out one digit "1" or "2" (he doesn’t know the others), and Alice writes the number into any empty cell of any bill and shows the result to Basilio. When all the cells are filled, Basilio takes as many bills with different numbers as possible (out of several with the same number, he takes only one), and the rest is taken by Alice. What is the largest number of bills Basilio can get, regardless of Alice’s actions?