Problems

Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.

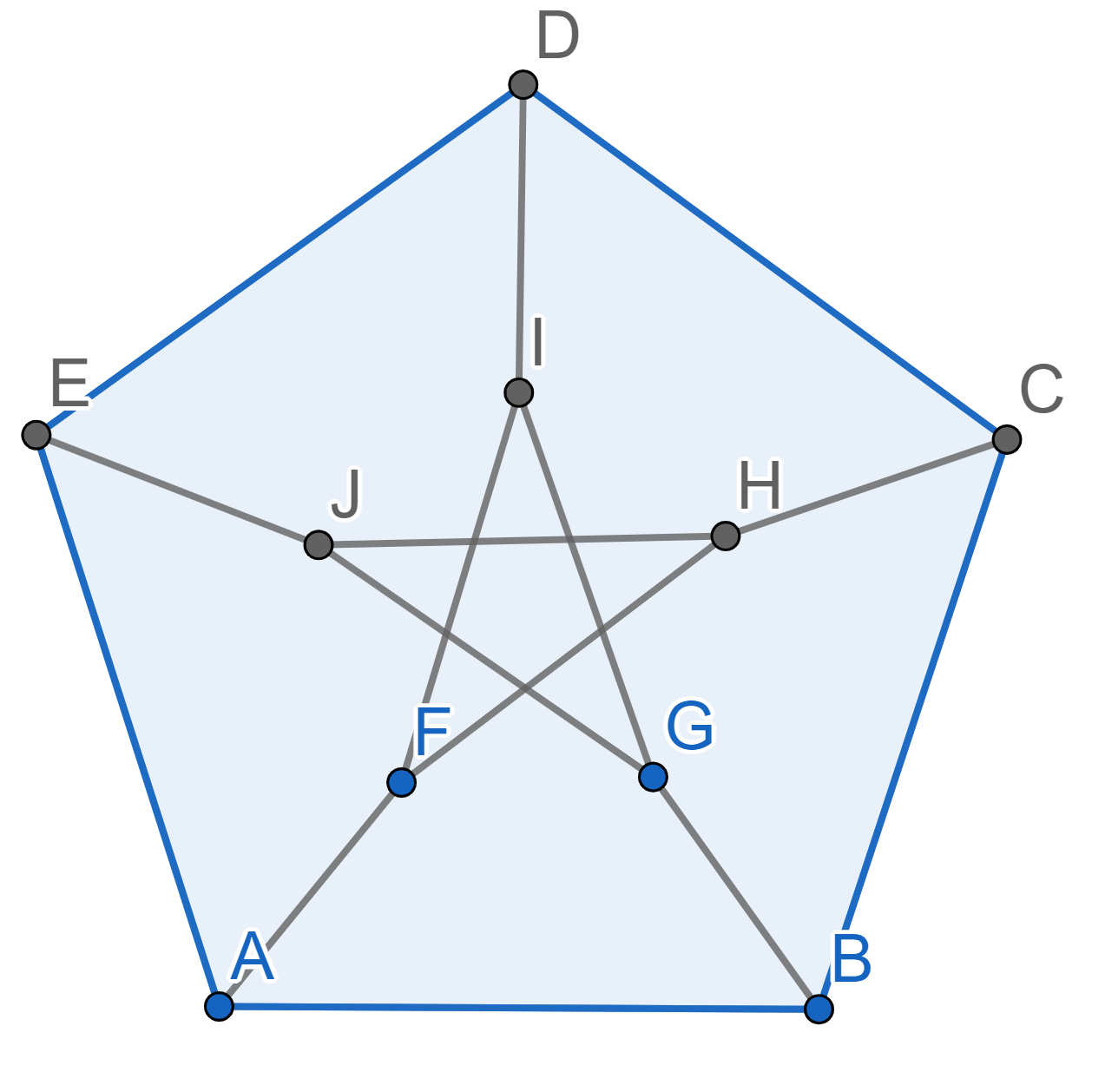
We want to color each of the 15 segments in the picture below using three colors. We need to color them so that if two segments share a point, then they are not the same color. For example, you cannot have both \(AB\) and \(BC\) be blue since they share the end \(B\). Is such a painting possible?

In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?

An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.

A monkey becomes happy when they eat three different fruits. What is the largest number of monkeys that can become happy with \(20\) pears, \(30\) bananas, \(40\) peaches and \(50\) tangerines?

For any real number \(x\), the absolute value of \(x\), written \(\left| x \right|\), is defined to be \(x\) if \(x>0\) and \(-x\) if \(x \leq 0\). What are \(\left| 3 \right|\), \(\left| -4.3 \right|\) and \(\left| 0 \right|\)?

Let \(x\) and \(y\) be real numbers. Prove that \(x \leq \left| x \right|\) and \(0 \leq \left| x \right|\). Then prove that the following inequality holds \(\left| x+y \right| \leq \left| x \right|+\left| y \right|\).

There are \(n\) balls labelled 1 to \(n\). If there are \(m\) boxes labelled 1 to \(m\) containing the \(n\) balls, a legal position is one in which the box containing the ball \(i\) has number at most the number on the box containing the ball \(i+1\), for every \(i\).

There are two types of legal moves: 1. Add a new empty box labelled \(m+1\) and pick a box from box 1 to \(m+1\), say the box \(j\). Move the balls in each box with (box) number at least \(j\) up by one box. 2. Pick a box \(j\), shift the balls in the boxes with (box) number strictly greater than \(j\) down by one box. Then remove the now empty box \(m\).

Prove it is possible to go from an initial position with \(n\) boxes with the ball \(i\) in the box \(i\) to any legal position with \(m\) boxes within \(n+m\) legal moves.

Given a natural number \(n\), find a formula for the number of \(k\) less than \(n\) such that \(k\) is coprime to \(n\). Prove that the formula works.

Scrooge McDuck has \(100\) golden coins on his office table. He wants to distribute them into \(10\) piles so that no two piles contain the same amount of coins. Moreover, no matter how you divide any of the piles into two smaller piles, among the resulting \(11\) piles there will be two with the same amount of coins. Find an example of how he could do that.

Let \(A=\{1,2,3\}\) and \(B=\{2,4\}\) be two sets containing natural numbers. Find the sets: \(A\cup B\), \(A\cap B\), \(A-B\), \(B-A\).

Let \(A=\{1,2,3,4,5\}\) and \(B=\{2,4,5,7\}\) be two sets containing natural numbers. Find the sets: \(A\cup B\), \(A\cap B\), \(A-B\), \(B-A\).