Problems

Peter went to the Museum of Modern Art and saw a square painting in a frame of an unusual shape. The frame consisted of \(21\) congruent triangles. Peter was interested in what the angles of these triangles were equal to. Help him find these angles.

Red, blue and green chameleons live on an island. One day \(35\) chameleons stood in a circle. A minute later, they all changed colour at the same time, each changing into the colour of one of their neighbours. A minute later, everyone again changed their colours at the same time into the colour of one of their neighbours. Is it ever possible that each chameleon was each of the colours red, blue and green at some point? For example, it’s allowed for a chameleon to start off blue, turn green after one minute, then turn red after the second minute. It’s not allowed for a chameleon to start off blue, turn green after one minute, but then turn back to blue after the second minute.

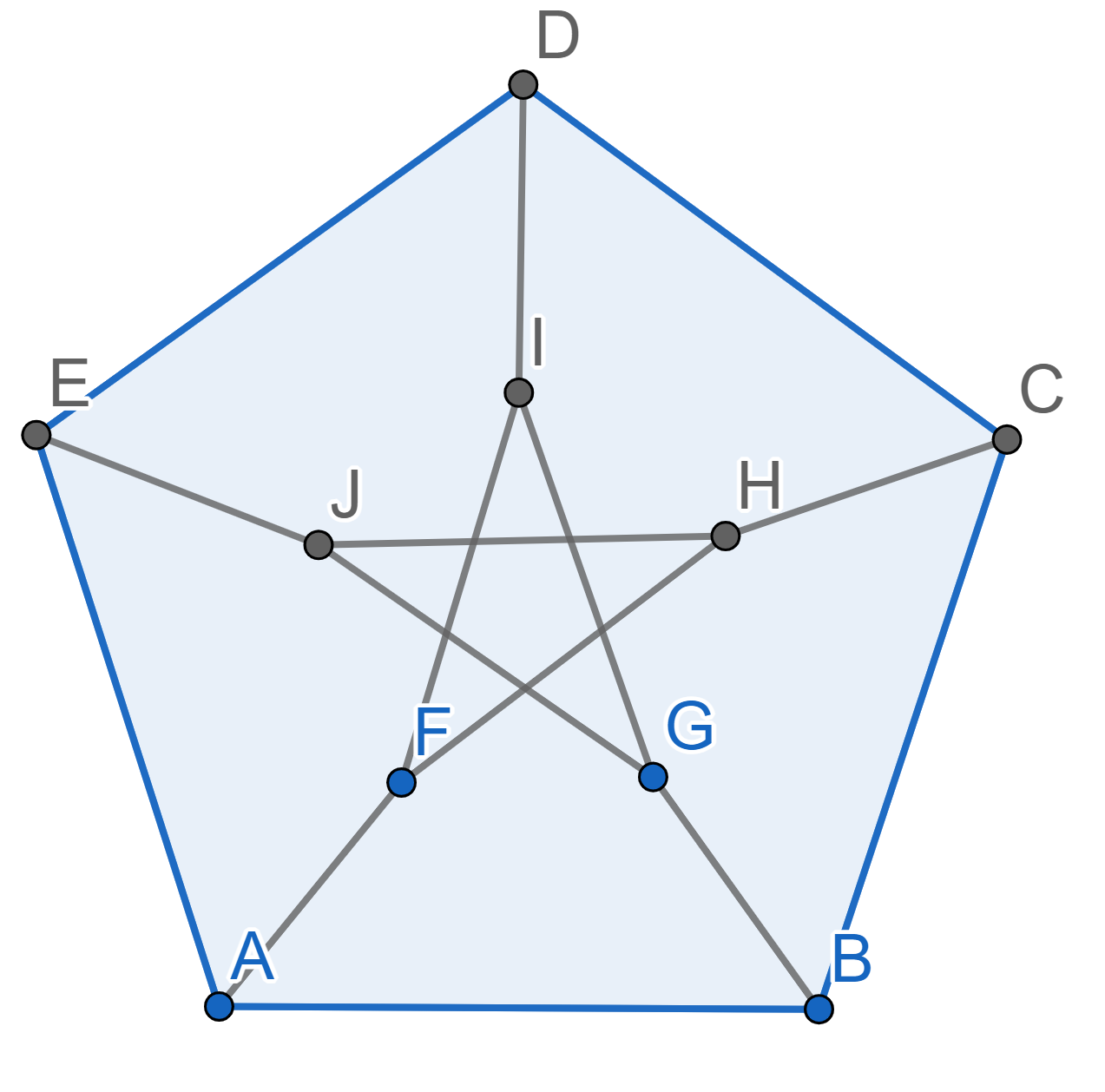
We wish to paint the \(15\) segments in the picture below in three colours. We want it such that no two segments of the same colour have a common end. For example, you cannot have both \(AB\) and \(BC\) blue since they share the end \(B\). Is such a painting possible?

In an \(n\times n\) table, two opposite corner squares are black and the rest are white. We wish to turn the whole \(n\times n\) table black in two stages. In the first stage, we paint black some of the squares that are white at the moment. In the second stage, we can perform the following two operations as much as we like. The row operation is to swap the colours of all the squares in a particular row. The column operation is to swap the colours of all the squares in a particular column. What is the fewest number of white squares that we can paint in the first stage?

An example of the row operation: let W stand for white and B stand for black and suppose that \(n=5\). Also suppose that a particular row has the colours WWBWB. Then performing the row operation would change this row to BBWBW.

A monkey becomes happy when they eat three different fruits. What is the largest number of monkeys that can become happy with \(20\) pears, \(30\) bananas, \(40\) peaches and \(50\) tangerines?

Let’s play some games today! We will play a classic game known as nim, which is thought to be one of the oldest games.

Typically people play nim using matchsticks, though stones and coins are popular too. There are a few heaps of matchsticks in nim. Players take turns to remove matchsticks from a heap of their choosing. The player can remove any number of matchsticks they wish from that heap. Whoever has no matchsticks left to take loses.

This following position will be written as \(\text{Nim}(3,3,3)\):

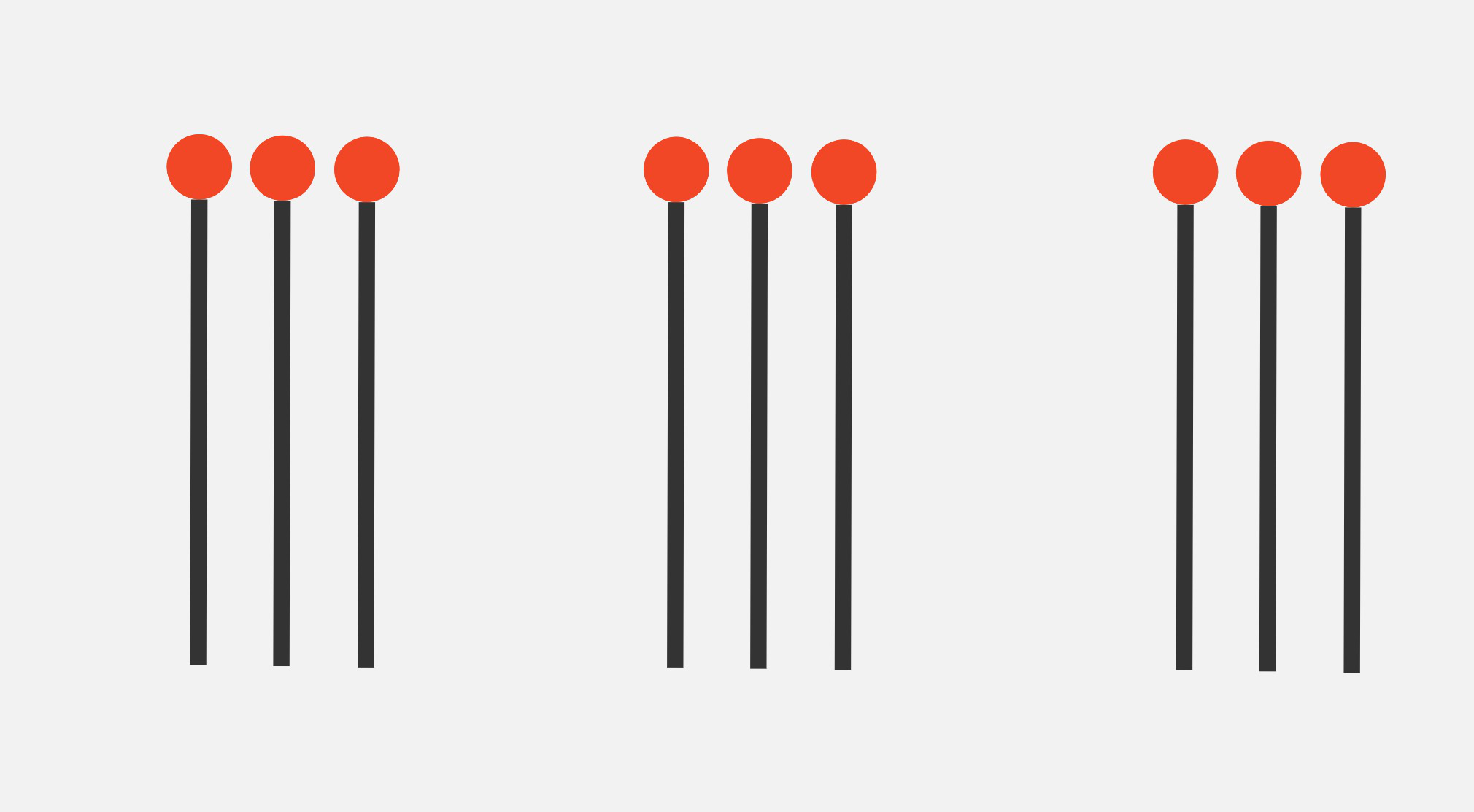
As another example, this is \(\text{Nim}(1,2,3,4)\):

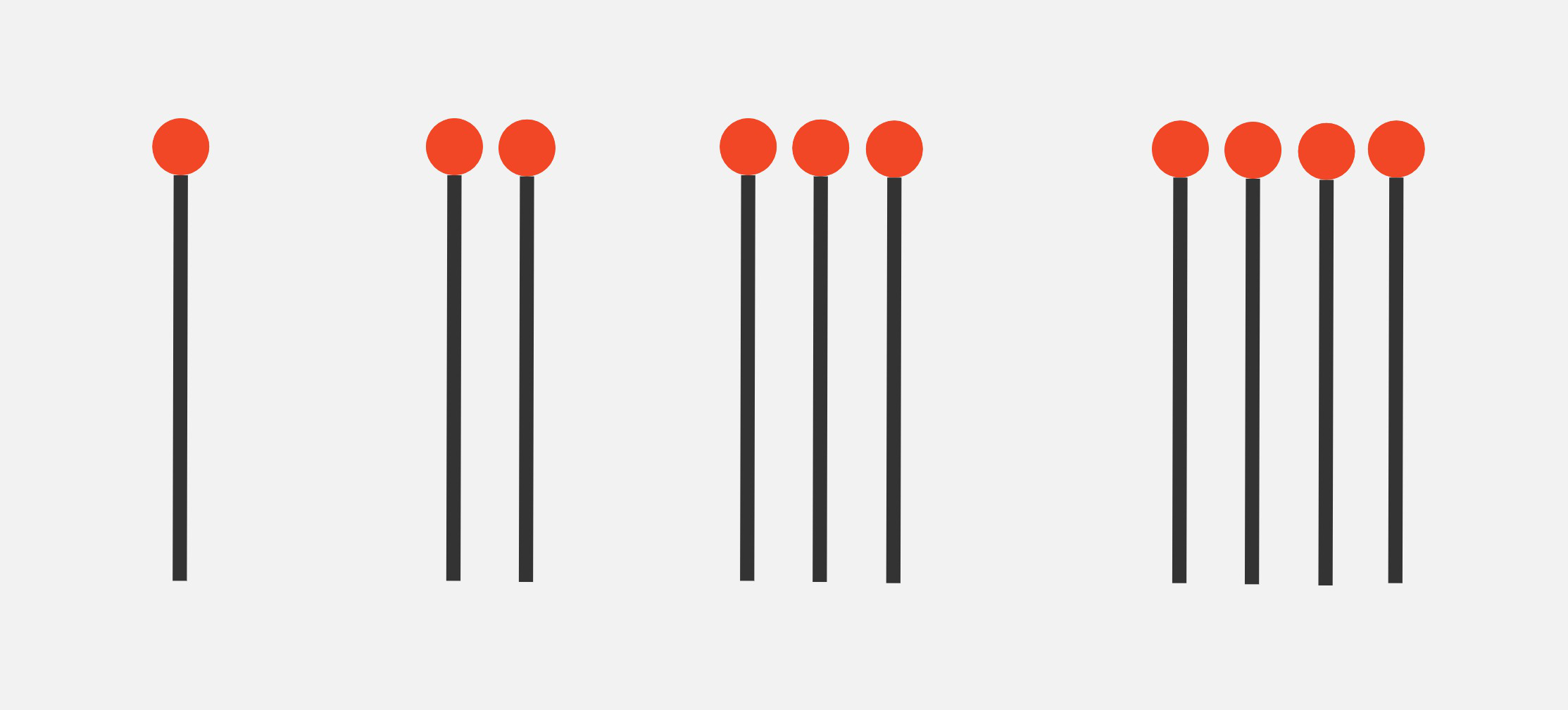
We will omit heaps of size zero, so \(\text{Nim}(3,0,3,0,3)\) is the same as \(\text{Nim}(3,3,3)\).

Nim is important because a large class of games are equivalent to it despite its simple appearance. The interested reader should look up “Sprague-Grundy Theorem".

Let us introduce a few terms that will be helpful for analyzing games. A game \(G\) consists of some positions and a set of rules. A position \(g\) in the game \(G\) is called a winning position if the player starting this turn has a winning strategy. This means as long as the player starting this turn continues to play optimally, the second player has to lose. Conversely, a position \(g\) is a losing position if the player starting this turn has no winning strategy.

Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:

Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.

This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).

Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.

Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).

Show that \(\text{Nim}(x,y,z)\) is a losing position if and only if \(x \oplus y \oplus z = 0\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).

Is \(\text{Nim}(7,11,15)\) a winning position or a losing position? If it is a winning position, what is the optimal move?