Problems
From the examples above, we see that we often need to pick \(k\) objects from \(n\) objects where the order of the \(k\) objects is ignored. The number of ways to pick them is notated with the special symbol \(\binom{n}{k}\), pronounced "\(n\) choose \(k\)". What’s a formula for \[\binom{n}{k}\]?
Find the mistake in the sequence of equalities: \(-1=(-1)^{\frac{2}{2}}=((-1)^2)^{\frac{1}{2}}=1^{\frac{1}{2}}=1\).
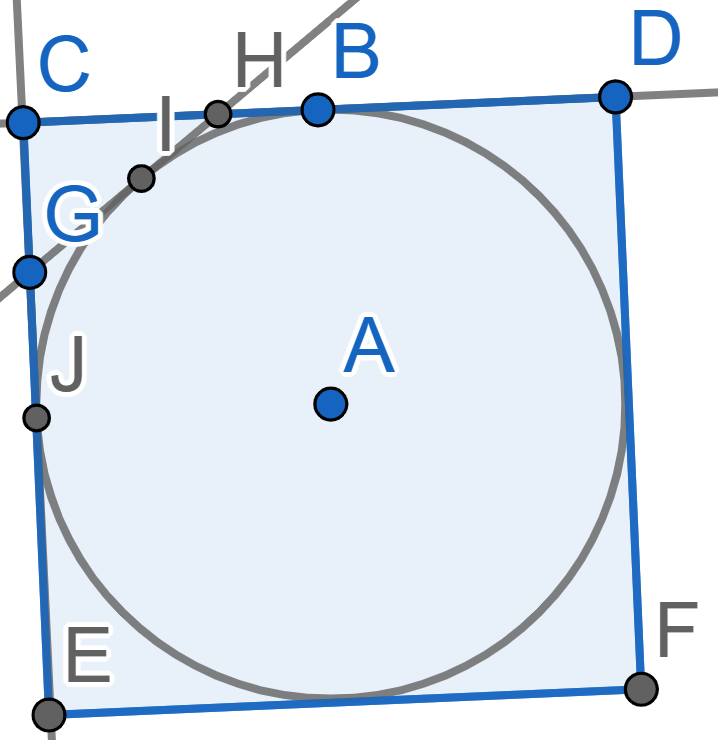
A circle with center \(A\) is inscribed into a square \(CDFE\). A line \(GH\) intersects the sides \(CD\) and \(CE\) of the square and is tangent to the circle at the point \(I\). Find the perimeter of the triangle \(CHG\) (the sum of lengths of all the sides) if the side of the square is \(10\)cm.
Suppose that \(p\) is a prime number. How many numbers are there less than \(p^2\) that are relatively prime to \(p^2\)?
Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:
| XOR | 0 | 1 |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 0 |
Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.
| 1 | 0 | 1 | 1 | 0 | |
| XOR | 0 | 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 |
This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).
Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.
Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Show that \(\text{Nim}(x,y,z)\) is a losing position if and only if \(x \oplus y \oplus z = 0\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Is \(\text{Nim}(7,11,15)\) a winning position or a losing position? If it is a winning position, what is the optimal move?
Show that \(\text{Nim}(x_1,\dots,x_k)\) is an losing position if and only if \(x_1 \oplus \dots \oplus x_k = 0\). \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).
Imagine the Earth is a perfectly round solid ball. Let us drill from the North Pole, London and Beijing simultaneously and meet at the centre of Earth. A ball with three openings is formed. The surface of this ball is shown on the left of the picture below. Describe how to stretch this surface so that it looks like the surface of a donut with two holes as shown on the right.
