Problems

How many permutations of 13 cards leaves the third card where it started?

Does there exist an irreducible tiling with \(1\times2\) rectangles of a \(6\times 6\) rectangle?

Irreducibly tile a floor with \(1\times2\) tiles in a room that is a \(6\times8\) rectangle.

Let \(m\) and \(n\) be positive integers. What positive integers can be written as \(m+n+\gcd(m,n)+\text{lcm}(m,n)\), for some \(m\) and \(n\)?

Suppose that \(n\) is a natural number and \(p\) is a prime number. How many numbers are there less than \(p^n\) that are relatively prime to \(p^n\)?

Let \(n\) be a positive integer. We denote by \(s(n)\) the sum of the divisors of \(n\). For example, the divisors of \(n=6\) are \(1\), \(2\), \(3\) and \(6\), so \(s(6)=1+2+3+6=12\). Prove that, for all \(n\ge1\), \[\sum_{k=1}^ns(k)=s(1)+s(2)+...+s(n)\le\frac{\pi^2}{12}n^2+\frac{n\log n}{2}+\frac{n}{2}.\]

Consider a line segment of length \(3m\). Jack chose \(4\) random points on the segment and measured all the distances between those \(4\) points. Prove that at least one of the distances is less than or equal to \(1m\).

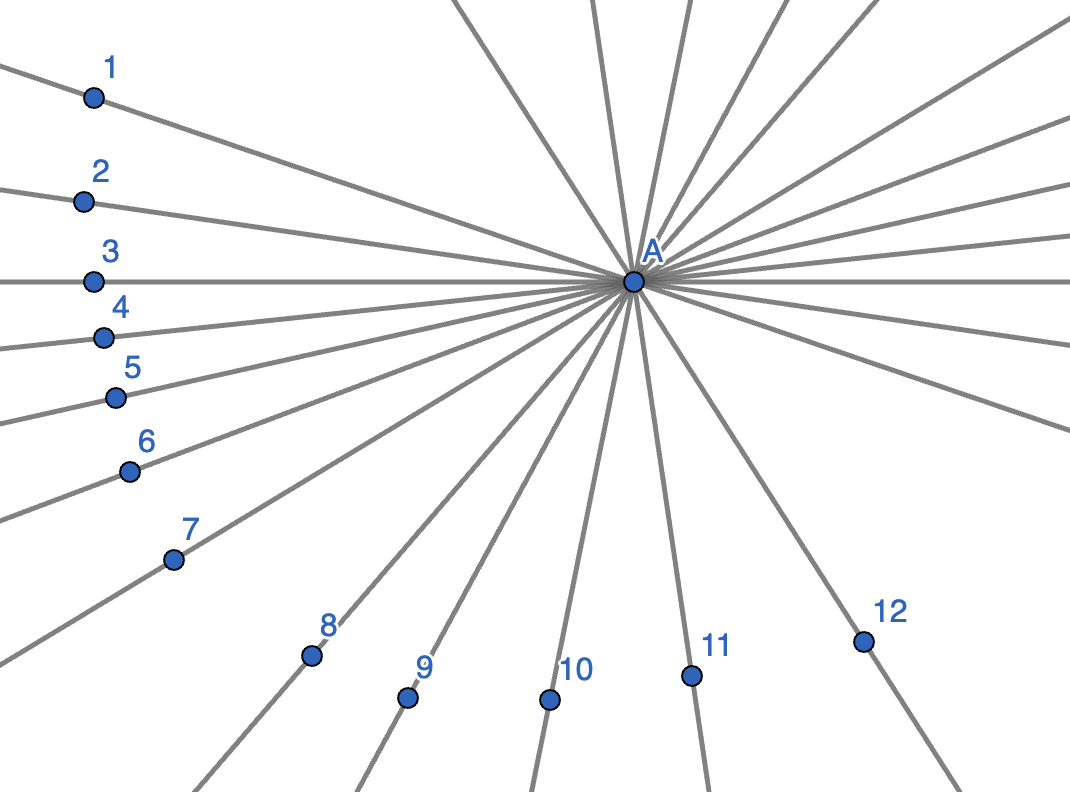
Twelve lines are drawn on the plane, passing through a point \(A\). Prove that there are two of them with angle less than \(17^{\circ}\) between them.

Inside a square of area \(6\), there are three polygons, each of area \(3\). Show that some two of these polygons overlap and the area of the overlap is at least \(1\).

A Wimbledon doubles court is \(78\)ft\(\times36\)ft. After a long practice match, there were \(79\) tennis balls in the court area. Show that some two of the balls were at most \(6\sqrt{2}\)ft away from each other.