Problems

Show how five queens can dominate a standard \(8\times8\) chessboard. That is, each square is attacked by some queen.

How many independent queens can you place on a \(5\times5\) grid? That is, so none of them attack each other.

How many ways can you place \(8\) rooks independently on a chessboard? That is, so that none of them attack each other.

Why are there no closed knight’s tours on an \(n\times n\) grid when \(n\) is odd? A knight’s tour is closed if you can get to the first square from the last square by a knight’s move.

Show how to place fourteen dominating bishops on a standard \(8\times8\) chessboard. That is, every square either contains a bishop, or is attacked by some bishop.

Place eight independent queens on a standard \(8\times8\) chessboard.

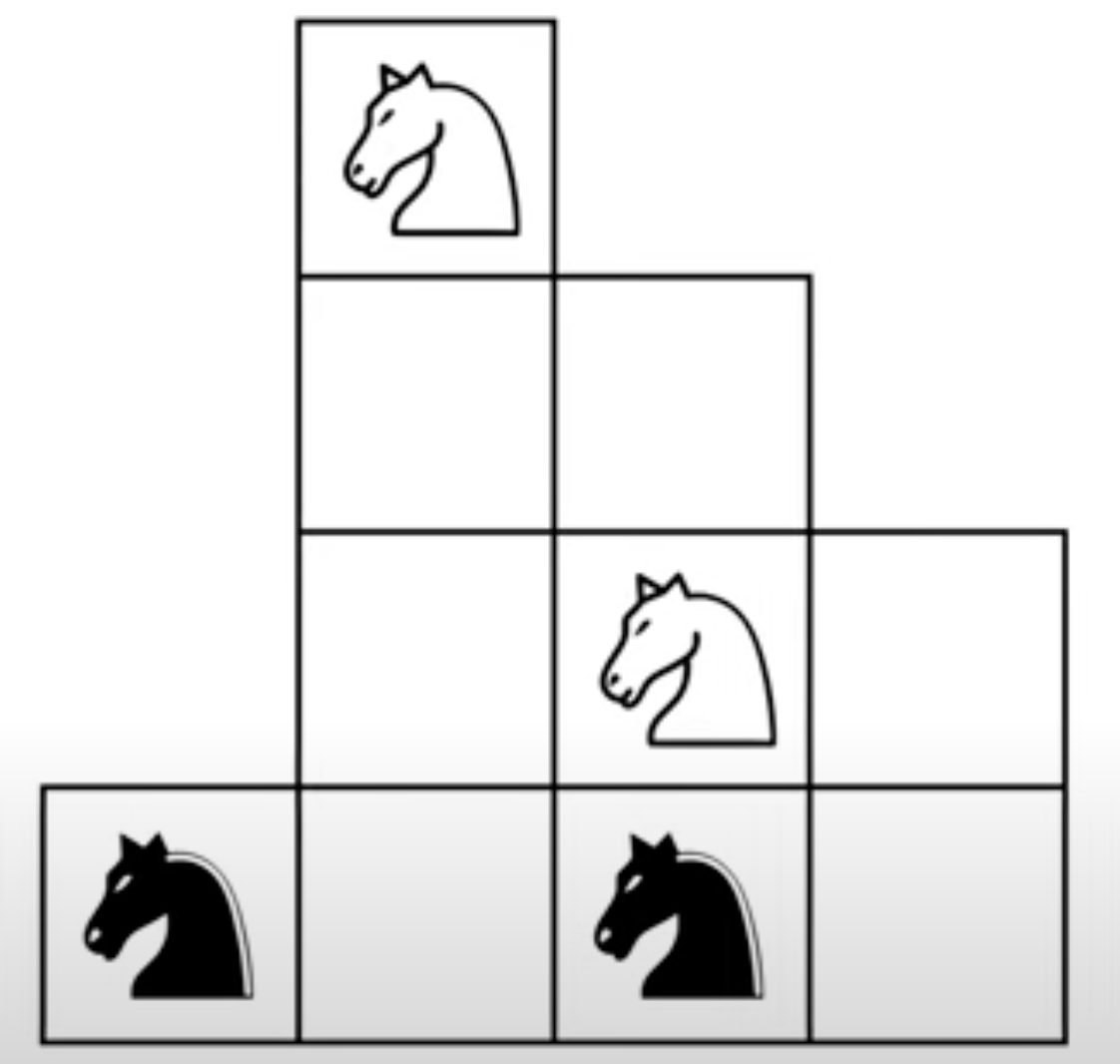
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.