Problems
Explain why you can’t rotate the sides on a normal Rubik’s cube to get to the following picture (with no removing stickers, painting, or other cheating allowed).

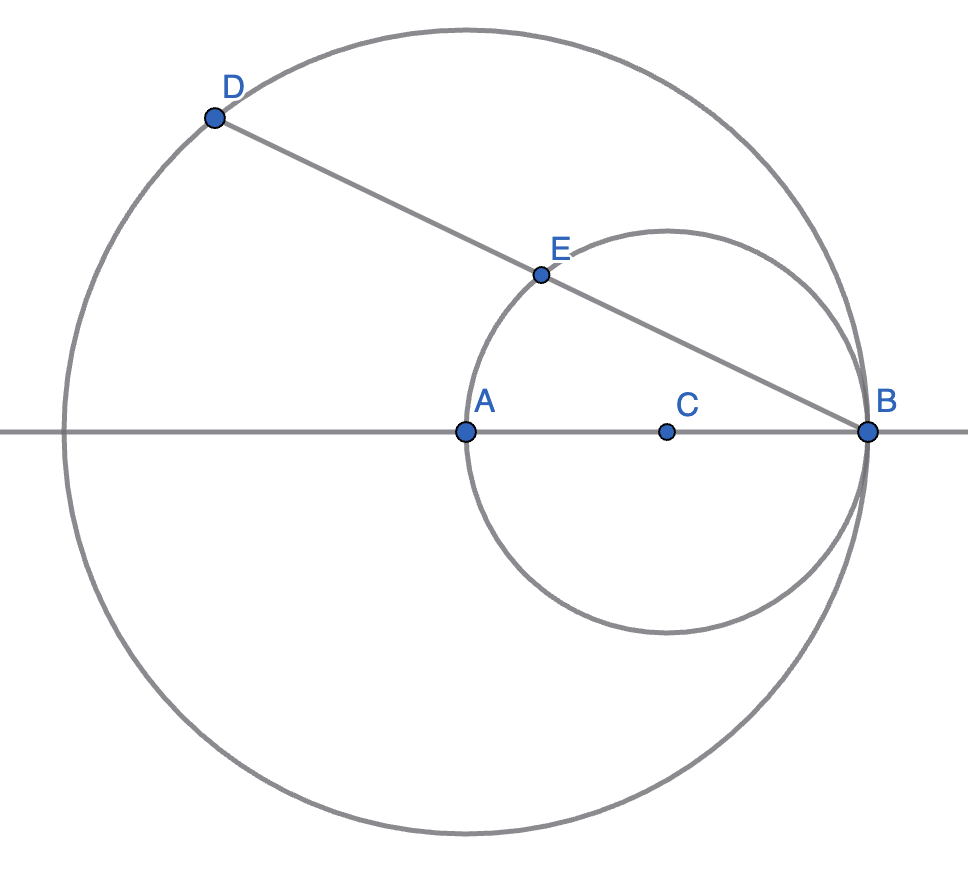
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
Are there any two-digit numbers which are the product of their digits?
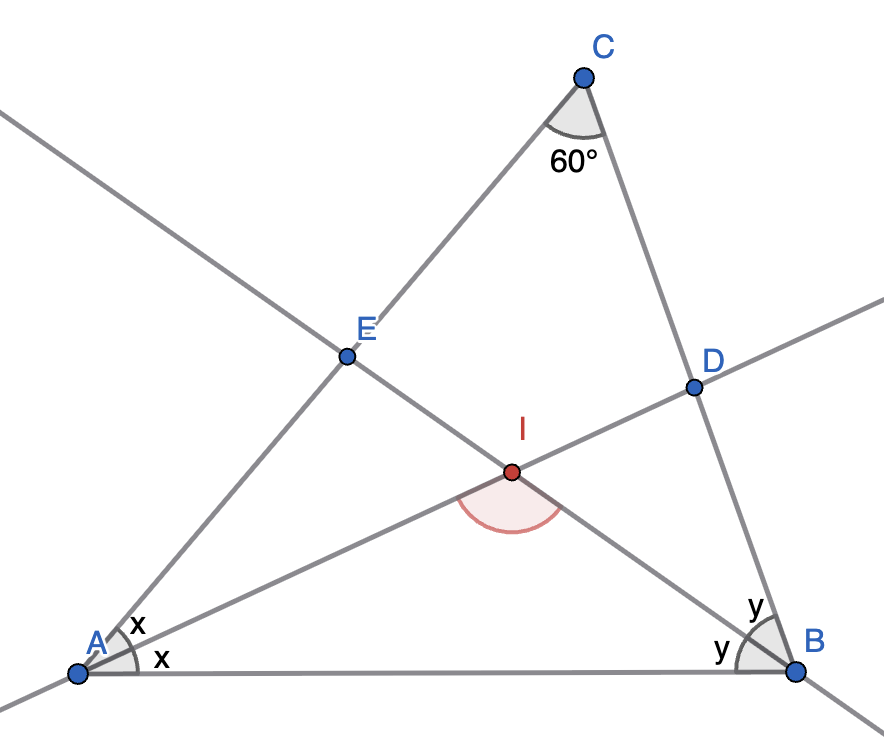
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).
Find the angle \(\angle AIB\), marked in red.
Find, with proof, all integer solutions of \(a^3+b^3=9\).
Suppose that \((x_1,y_1),(x_2,y_2)\) are solutions to Pell’s equation \(x^2-dy^2 = 1\). Show that \((x_1x_2+dy_1y_2,x_1y_2+x_2y_2)\) also satisfies the same equation.
Suppose that \(x+y\sqrt{d}>1\) gives a solution to Pell’s equation. Show that \(x\geq 2\) and \(y\geq 1\). Can the bounds be achieved?
Let \(x,x',y,y'\) be integers such that \(x+\sqrt{d}y=x'+\sqrt{d}y'\), where \(d\) is a number that is not a square. Show that \(x=x'\) and \(y=y'\).
Show that if \(u_1\) and \(u_2\) are solutions to Pell’s equation, then \(u_1u_2\) is also a solution to Pell’s equation. What can you conclude about the number of solutions, if there are any?