Problems
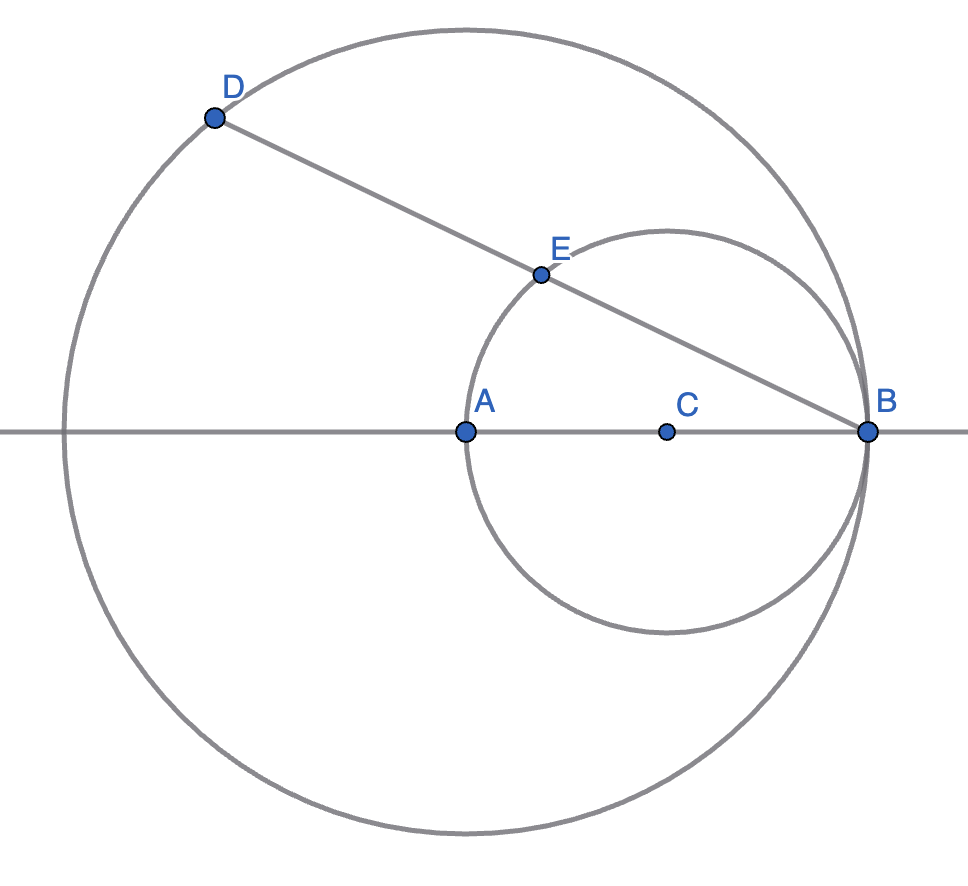
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
Are there any two-digit numbers which are the product of their digits?
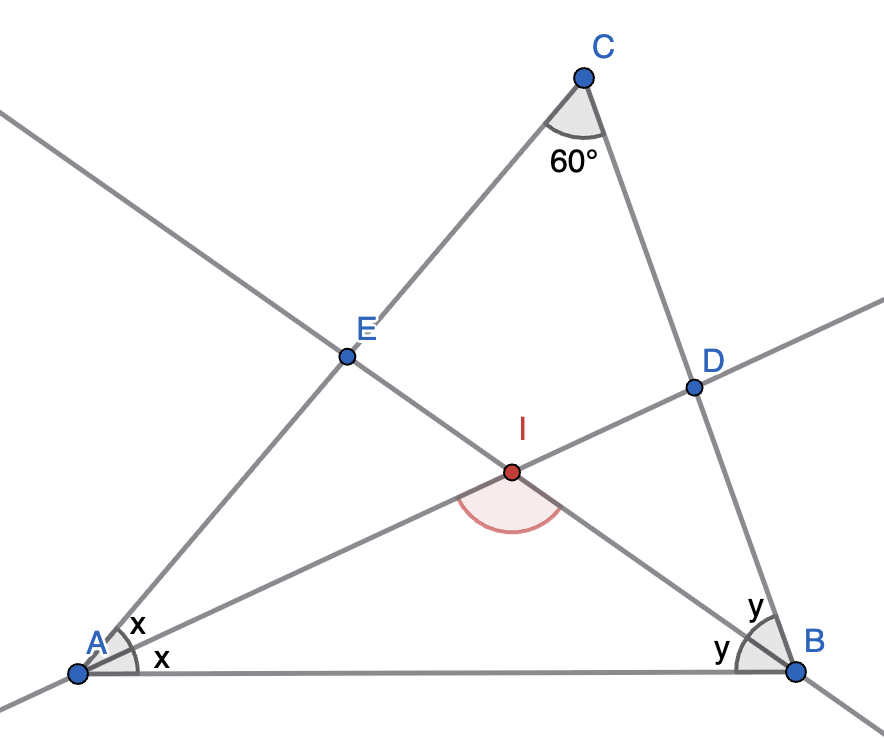
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).
Find the angle \(\angle AIB\), marked in red.
Find, with proof, all integer solutions of \(a^3+b^3=9\).
An equation of the form \(x^2 - dy^2 = 1\) where \(d>0\) is a nonsquare (what if \(d\) is a square?) integer and we seek \(x,y\) in the integers is called Pell’s equation. By changing the sign of \(x\) and \(y\), we may assume they are nonnegative. There is always the solution \((x,y)=(1,0)\) which we call trivial.
Here is a useful way to think about the solutions to Pell’s equations. The difference of squares identity prompts us to consider the solution \((x,y)\) to Pell’s equation as the real number \(x+y\sqrt{d}\). The fact that \((x,y)\) is a solution simply means \((x+y\sqrt{d})(x-y\sqrt{d})=1\).
Here is some common notation you might see if you look at books or on the internet: if we have a number \(u=x+y\sqrt{d}\), we can define its conjugate as the number \(\bar u=x-y\sqrt{d}\). Moreover, the set of numbers of the form \(x+y\sqrt{d}\) where \(x,y\) are whole numbers, is often written as \(\mathbb Z[\sqrt{d}]\) (pronounced “integers adjoint \(\sqrt{d}\)"). Therefore, a number \(u\) that belongs to \(\mathbb Z[\sqrt{d}]\) is a solution to Pell’s equation if \(u\bar u=1\).
As with all Diophantine equations, we would like to to know the following about Pell’s equation.
Does Pell’s equation always have nontrivial solutions?
When Pell’s equation does have solutions, is the number of solutions finite?
How can we describe all solutions to Pell’s equation?
In this sheet, we answer all of the questions above and apply these theoretical results to some other problems.
Suppose that \((x_1,y_1),(x_2,y_2)\) are solutions to Pell’s equation \(x^2-dy^2 = 1\). Show that \((x_1x_2+dy_1y_2,x_1y_2+x_2y_2)\) also satisfies the same equation.
Suppose that \(x+y\sqrt{d}>1\) gives a solution to Pell’s equation. Show that \(x\geq 2\) and \(y\geq 1\). Can the bounds be achieved?
Let \(x,x',y,y'\) be integers such that \(x+\sqrt{d}y=x'+\sqrt{d}y'\), where \(d\) is a number that is not a square. Show that \(x=x'\) and \(y=y'\).
Show that if \(u_1\) and \(u_2\) are solutions to Pell’s equation, then \(u_1u_2\) is also a solution to Pell’s equation. What can you conclude about the number of solutions, if there are any?
Find all integer solutions to \(x^2+y^2-1=4xy\).