Problems
In a bag we have \(99\) red balls and \(99\) blue balls. We take balls from the bag, two balls at a time:
If the two balls are of the same colour, then we put in a red ball to the bag.
If the two balls are of different colour, we return a blue ball to the bag.
Regardless, after each step, one ball is lost from the bag, so eventually there will be only one ball. What is the colour of this last ball?
You have an \(8\times 8\) chessboard coloured in the usual way. You can pick any two adjacent squares (i.e: any \(2\times 1\) or \(1\times 2\) section of the board) and flip the white tiles to black tiles and vice-versa. Is it possible to finish with \(63\) white pieces and \(1\) black piece?
We start with the point \((1,3)\) of the plane. We generate a sequence of points with the following rule: the \(x\)-coordinate of the new point is the arithmetic mean of the \(x\) and \(y\) coordinates of the previous point, and the \(y\)-coordinate of the new point is the harmonic mean of the \(x\) and \(y\) coordinates of the previous points. The harmonic mean of two numbers \(x\) and \(y\) is \(\frac{2}{\frac{1}{x} + \frac{1}{y}}\). Is the point \((3,2)\) in the sequence?
Four black dots are drawn on a whiteboard. On the dots we write the numbers \(10\), \(20\), \(30\), and \(40\) (one number on each dot). We then repeat the following move any number of times: choose one dot, decrease its number by \(3\), and increase the number on each of the other three dots by \(1\). After some number of moves, is it possible for all four dots to show the number \(25\) simultaneously?
Every year the citizens of the planet “Lotsofteeth" enter a contest
to see who has the most teeth.
This year the judge notices:
Nobody has 0 teeth (everyone has at least 1).
There are more people in the contest than the most teeth that any one person has. (For example, if the most teeth anyone has is 27, then there are more than 27 people participating in the contest.)
Must there be two people who have exactly the same number of teeth? Explain why.
Fred and George each had a square cake. Both of them made two straight cuts across their cake, from edge to edge. How could it happen that Fred ended up with three pieces, while George ended up with four?
Remember that two shapes are congruent if they are the same in shape and size, even if one is flipped or turned around. For example, here are two congruent shapes:

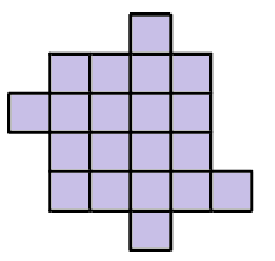
Cut the following shape into four congruent figures:
A cube net is a 2D shape that can be folded into a cube. For example, in the following diagram we show a cube net and the steps that fold it into a cube:
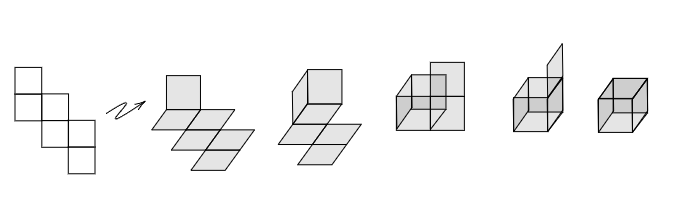
Imagine that you want to cover an endless floor with this cube net, so there are no gaps or overlaps, how would you lay them out? This is called covering or tiling the plane.
Cut a square into three parts and then use these three pieces to form a triangle such that:
All its angles are acute (i.e: less than \(90^\circ\)).
All its sides are of different lengths.
Jamie has a bag full of cards, where each card has a whole number written on it. How many cards must Jamie take from the bag to be certain that, among the cards chosen, there are at least two numbers whose average is also a whole number? Recall that to calculate the average of two numbers, we add them together and then divide by two.