Problems
Show that Pell’s equation \(x^2-dy^2=1\) has a nontrivial solution.
For the following equations, find the integer solution \((x,y)\) with the smallest possible absolute value of \(y\).
\(x^2 - 7y^2 = 1\);
\(x^2 - 7y^2 = 29\).
Find the integer solution \((x,y)\) with the smallest possible absolute value of \(y\). \(x^2 - 2y^2 = 1\);
This equation helps to find all the square-triangular numbers, namely all the numbers that are perfect squares and can be represented as the sum \(1+2+3+...m\) for some \(m\). Finding such a number is equivalent to finding a solution to the equation: \(2n^2 = m(m+1)\). Or finding a solution to the Pell’s equation \(x^2-2y^2 = 1\) for \(x=2m+1\), \(y=2n\).
Without using any wolves, show that Robinson’s goat can only graze shapes that are convex (that means, whenever you pick two points inside the shape, the whole line between them also lies inside). But if Robinson is allowed to use as many wolves as he likes, this restriction disappears. Show that in this case, he can make the goat graze in the shape of any polygon at all.
In a field, there are two pegs, \(A\) and \(B\), placed \(15\) metres apart. Each peg has a small
ring on top, and a rope can slide freely through these rings.
You have one rope and two goats that want to graze the grass, but they
will fight each other if they can both reach the same spot.
The rope may be arranged in any way you choose: it could pass through
both rings, only one, or neither, depending on your setup.
For what lengths of rope can you arrange things so that the goats cannot
fight each other?
Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?
There is a queue of \(n\) truth tellers and liars. The first person says, “more than half of us are liars". The second person says, “more than a quarter of us are liars". The third person says, “more than an eighth of us are liars", and so on, until the \(n\)th person says, “more than \(\frac{1}{2^n}\) of us are liars". Describe what the number of truth-tellers and liars could be, as well as their placement in the queue. Note that the solutions are not fixed numbers.
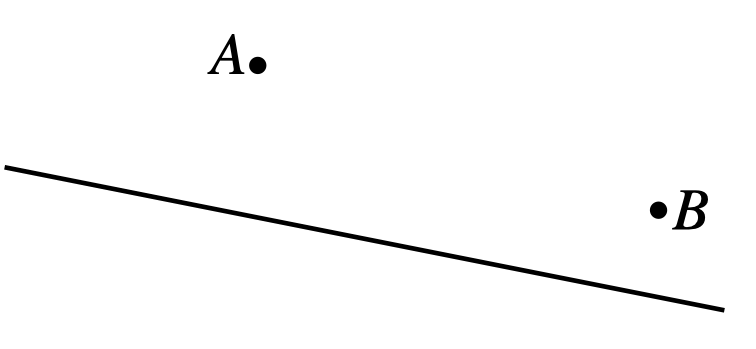
Fred starts running from point \(A\) and must reach point \(B\). On the way, he has to touch the fence shown as a straight line in the figure. It doesn’t matter where he touches the fence, as long as he does. What is the shortest path he can take?
Robbie and Paloma are playing football on a large, flat field. They both run at the same speed toward the ball. Where could the ball have been if Paloma reached it first?
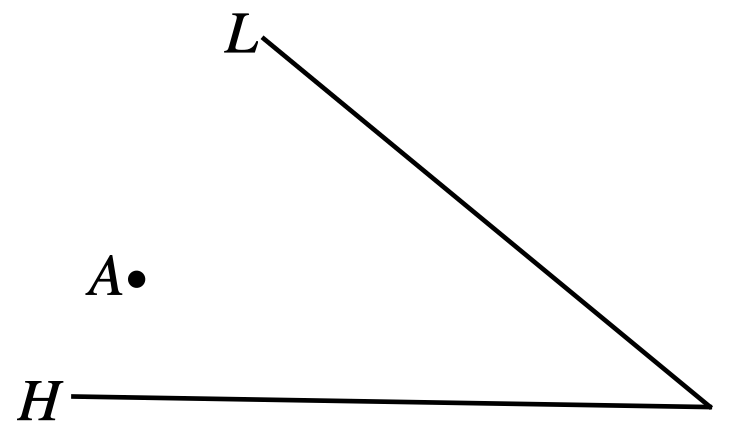
Oliver starts running from point \(A\) in the figure below. He must touch line \(H\), and then line \(L\). What is the shortest path he can take?