Problems

Long before meeting Snow White, the seven dwarves lived in seven different mines. There is an underground tunnel connecting any two mines. All tunnels were separate, so you could not start in one tunnel and somehow end up in another. Is it possible to walk through every tunnel exactly once without retracing your path?

The Pythagorean Theorem is one of the most important facts about geometry. It says that if we have a right-angled triangle (i.e: it has an angle of \(90^\circ\)), whose longest side measures \(C\), and its other two other sides measure \(A\) and \(B\):

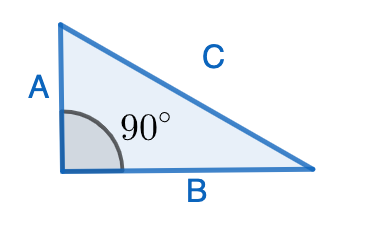
then \(A^2+B^2=C^2\). There are many proofs of this fact, and some involve dissections! Let’s have a look at the following two ways to dissect the same square:

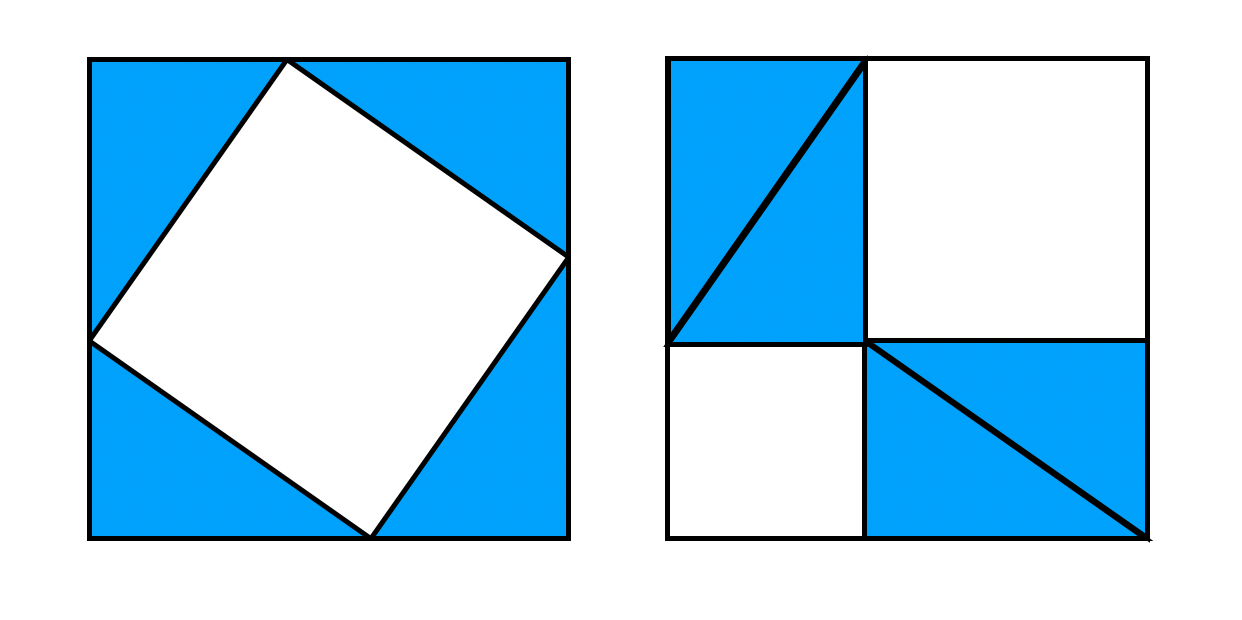
Can you explain how these dissections prove the Pythagorean Theorem?

Seven Smurfs live in seven mushroom houses. There is a tunnel between every pair of houses, so from any house you can walk to any other house. One of the Smurfs, Clumsy, starts walking from his house, but he must not use the same tunnel more than once. He keeps walking until he reaches a house where all the tunnels have already been used. Where will Clumsy’s journey end?

Suppose that \(x_1+y_1\sqrt{d}\) and \(x_2+y_2\sqrt{d}\) give solutions to Pell’s equation \(x^2-dy^2=1\) and \(x_1,x_2,y_1,y_2\geq 0\). Show that the following are equivalent:

1. \(x_1+y_1\sqrt{d} < x_2+y_2\sqrt{d}\),

2. \(x_1<x_2\) and \(y_1<y_2\),

3. \(x_1<x_2\) or \(y_1<y_2\).

If Pell’s equation \(x^2-dy^2 = 1\) has a nontrivial solution \((x_1,y_1)\), show that it has infinitely many distinct solutions.

Show that there are infinitely many triples of consecutive integers, each of which is a sum of the square of two integers.

Suppose that Pell’s equation \(x^2-dy^2=1\) has a solution \((x_1,y_1)\) where \(x_1,y_1\) are positive and \(y_1\) is minimal among all solutions with positive \(x,y\). Show that if \(x+y\sqrt{d}\) gives a solution to \(x^2-dy^2=1\), then \(x+y\sqrt{d}=\pm(x_1+y_1\sqrt{d})^k\) for some integer \(k\).

Suppose that \(x_1+y_1\sqrt{d}\) gives a solution to Pell’s equation \(x^2-dy^2=1\). Define a sequence \(x_n+y_n\sqrt{d} = (x_1+y_1\sqrt{d})^n\). Show that we have the recurrence relations \(x_{n+2} = 2x_1x_{n+1}-x_n\) and \(y_{n+2} = 2x_1y_{n+1}-y_n\).

Prove that the only solution to \(5^a-3^b=2\) with \(a,b\) being positive integers is \(a=b=1\).

Show that Pell’s equation \(x^2-dy^2=1\) has a nontrivial solution.