Problems

The polynomial \(P (x)\) of degree \(n\) has \(n\) distinct real roots.

What is the largest number of its coefficients that can be equal to zero?

For which \(\alpha\) does there exist a function \(f\colon \mathbb{R} \rightarrow \mathbb{R}\) that is not a constant, such that \(f (\alpha (x + y)) = f (x) + f (y)\)?

We are given a table of size \(n \times n\). \(n-1\) of the cells in the table contain the number \(1\). The remainder contain the number \(0\). We are allowed to carry out the following operation on the table:

1. Pick a cell.

2. Subtract 1 from the number in that cell.

3. Add 1 to every other cell in the same row or column as the chosen cell.

Is it possible, using only this operation, to create a table in which all the cells contain the same number?

Solve the equation \((x + 1)^3 = x^3\).

On a function \(f (x)\) defined on the whole line of real numbers, it is known that for any \(a > 1\) the function \(f (x)\) + \(f (ax)\) is continuous on the whole line. Prove that \(f (x)\) is also continuous on the whole line.

Does there exist a function \(f (x)\) defined for all \(x \in \mathbb{R}\) and for all \(x, y \in \mathbb{R}\) satisfying the inequality \(| f (x + y) + \sin x + \sin y | < 2\)?

We call a number \(x\) rational if it can be represented as \(x=\frac{p}{q}\) for coprime integers \(p\) and \(q\). Otherwise we call the number irrational.
Non-zero numbers \(a\) and \(b\) satisfy the equality \(a^2b^2 (a^2b^2 + 4) = 2(a^6 + b^6)\). Prove that at least one of them is irrational.

Prove that in any set of 117 unique three-digit numbers it is possible to pick 4 non-overlapping subsets, so that the sum of the numbers in each subset is the same.

The real numbers \(x\) and \(y\) are such that for any distinct prime odd \(p\) and \(q\) the number \(x^p + y^q\) is rational. Prove that \(x\) and \(y\) are rational numbers.

The functions \(f (x) - x\) and \(f (x^2) - x^6\) are defined for all positive \(x\) and increase. Prove that the function

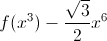
also increases for all positive \(x\).