Problems
Show that \(R(4,4)\ge18\) - that is, there’s a way of colouring the edges of \(K_{17}\) such that there’s no monochromatic \(K_4\).
Show that \(R(4,3)\le9\). That is, no matter how you colour the edge of \(K_9\), there must be a red \(K_4\) or a blue \(K_3\).
Show that \(R(4,4)\le18\) - that is, no matter how you colour the edges of \(K_{18}\), there must be a monochromatic \(K_4\).
By considering \(k-1\) copies of \(K_{k-1}\), show that \(R(k,k)\ge(k-1)^2\).
Let \(s>2\) and \(t>2\) be integers. Show that \(R(s,t)\le R(s-1,t)+R(s,t-1)\).
Using \(R(s,t)\le R(s-1,t)+R(s,t-1)\), prove that \(R(k,k)\le 4^k\).
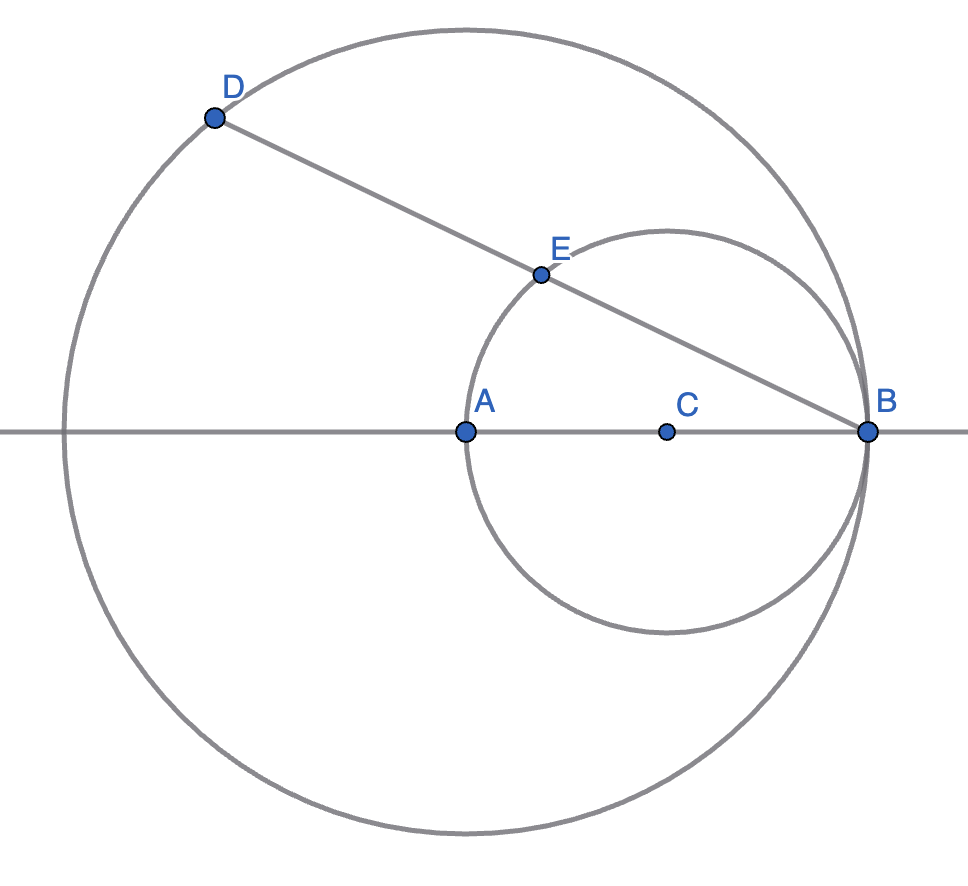
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
Are there any two-digit numbers which are the product of their digits?
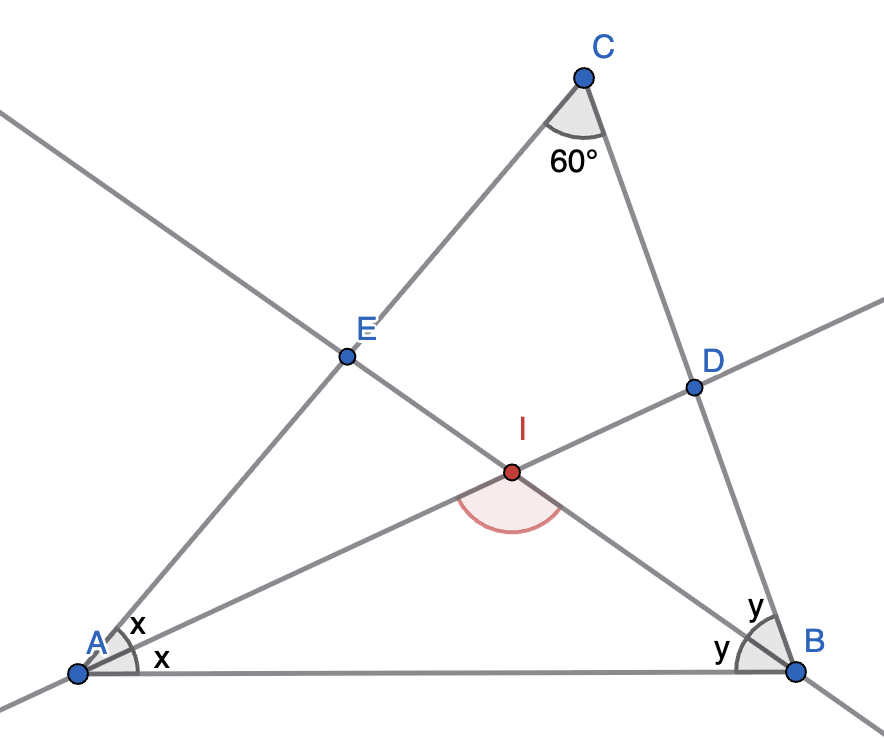
In the triangle \(\triangle ABC\), the angle \(\angle ACB=60^{\circ}\), marked at the top. The angle bisectors \(AD\) and \(BE\) intersect at the point \(I\).
Find the angle \(\angle AIB\), marked in red.