Problems
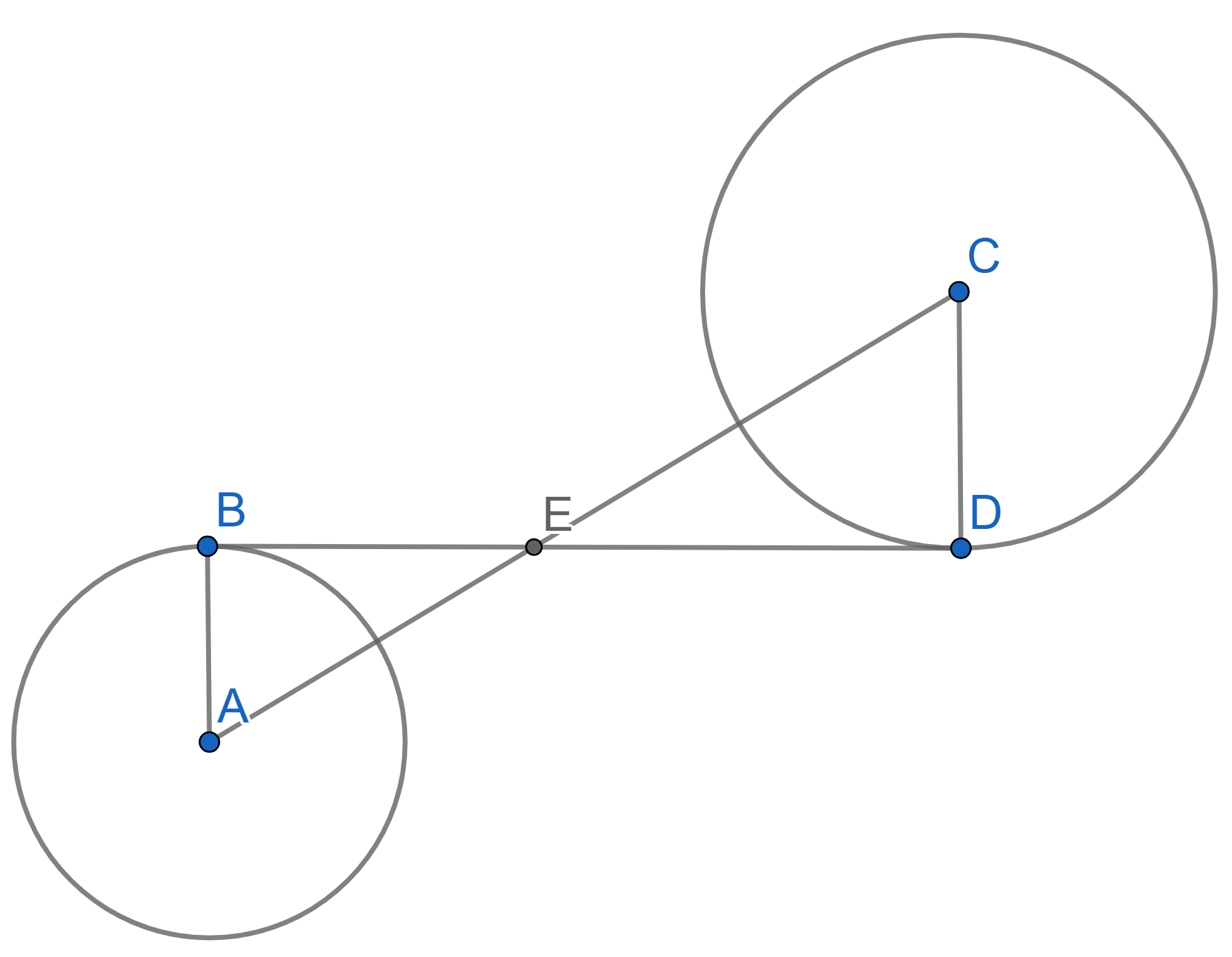
Given two circles, one has centre \(A\) and radius \(r\), another has centre \(C\) and radius \(R\). Both circles are tangent to a line at the points \(B\) and \(D\) respectively and the angles \(\angle CED = \angle AEB = 30^{\circ}\). Find the length of \(AC\) in terms of \(r\) and \(R\).
Consider a triangle \(CDE\). The lines \(CD\), \(DE\), and \(CE\) are tangent to a circle with centre \(A\) at the points \(F,G\), and \(B\) respectively. We also have that the angle \(\angle DCE = 120^{\circ}\). Prove that the length of the segment \(AC\) equals the perimeter of the triangle \(CDE\).
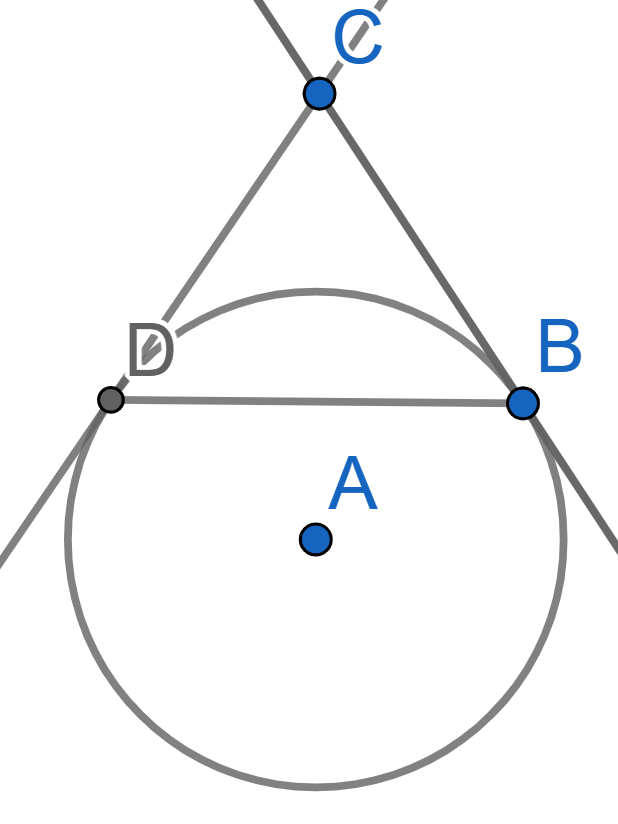
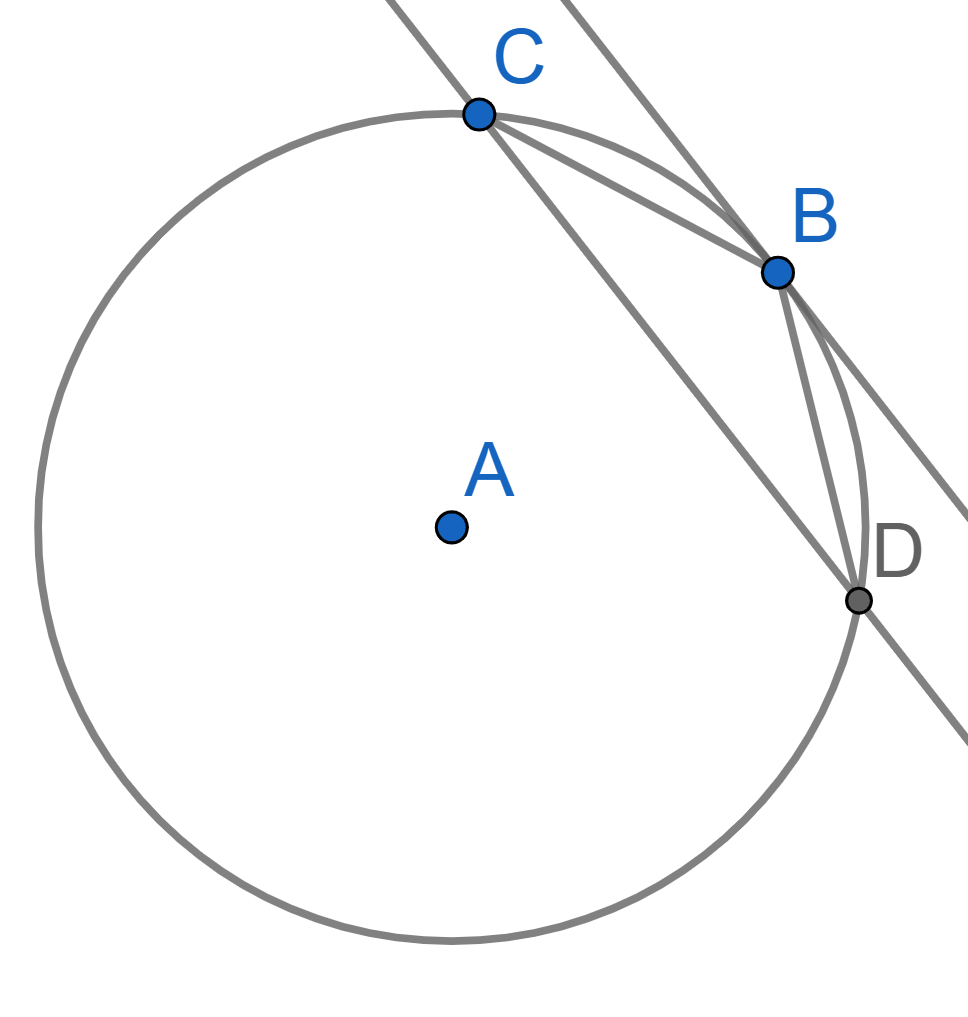
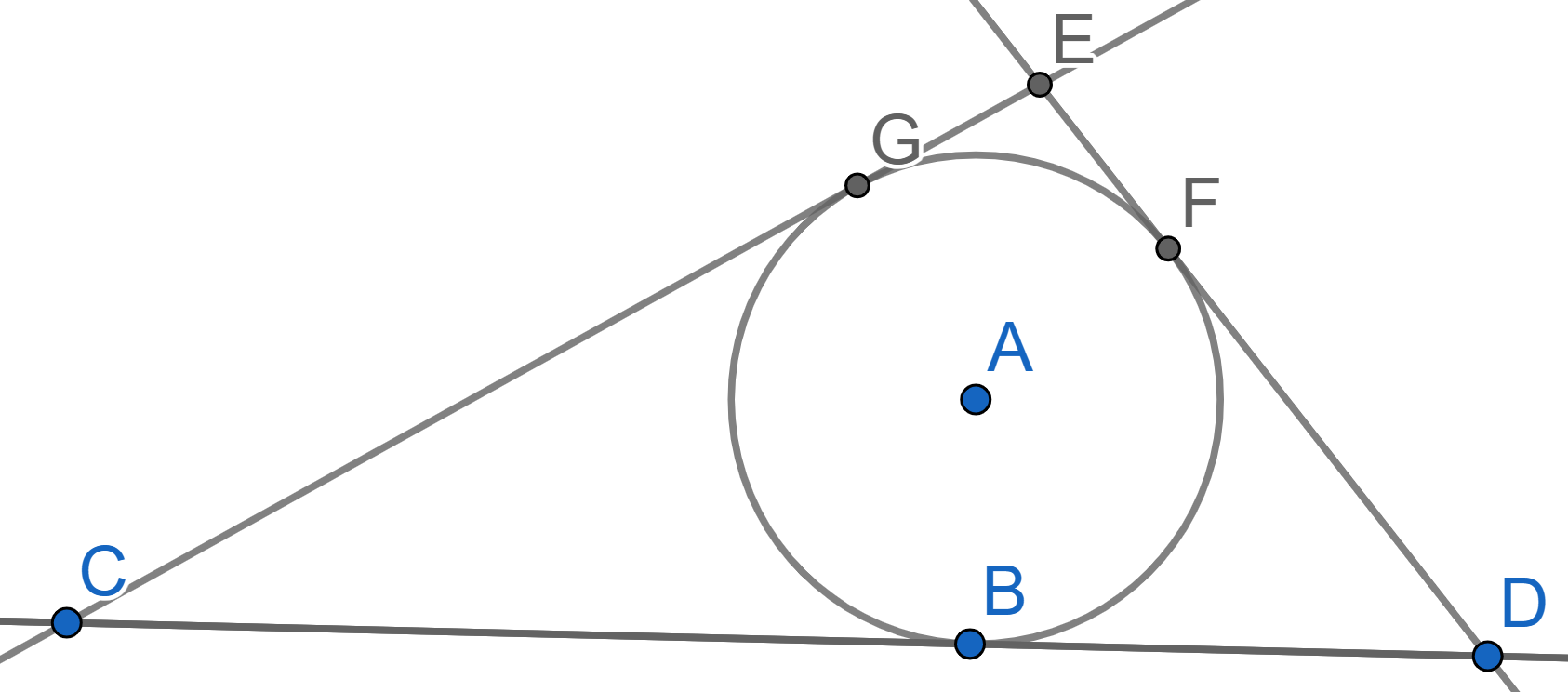
A circle with center \(A\) is tangent to the lines \(CB\) and \(CD\), see picture. Find the angles of the triangle \(BCD\) if \(BD=BC\).
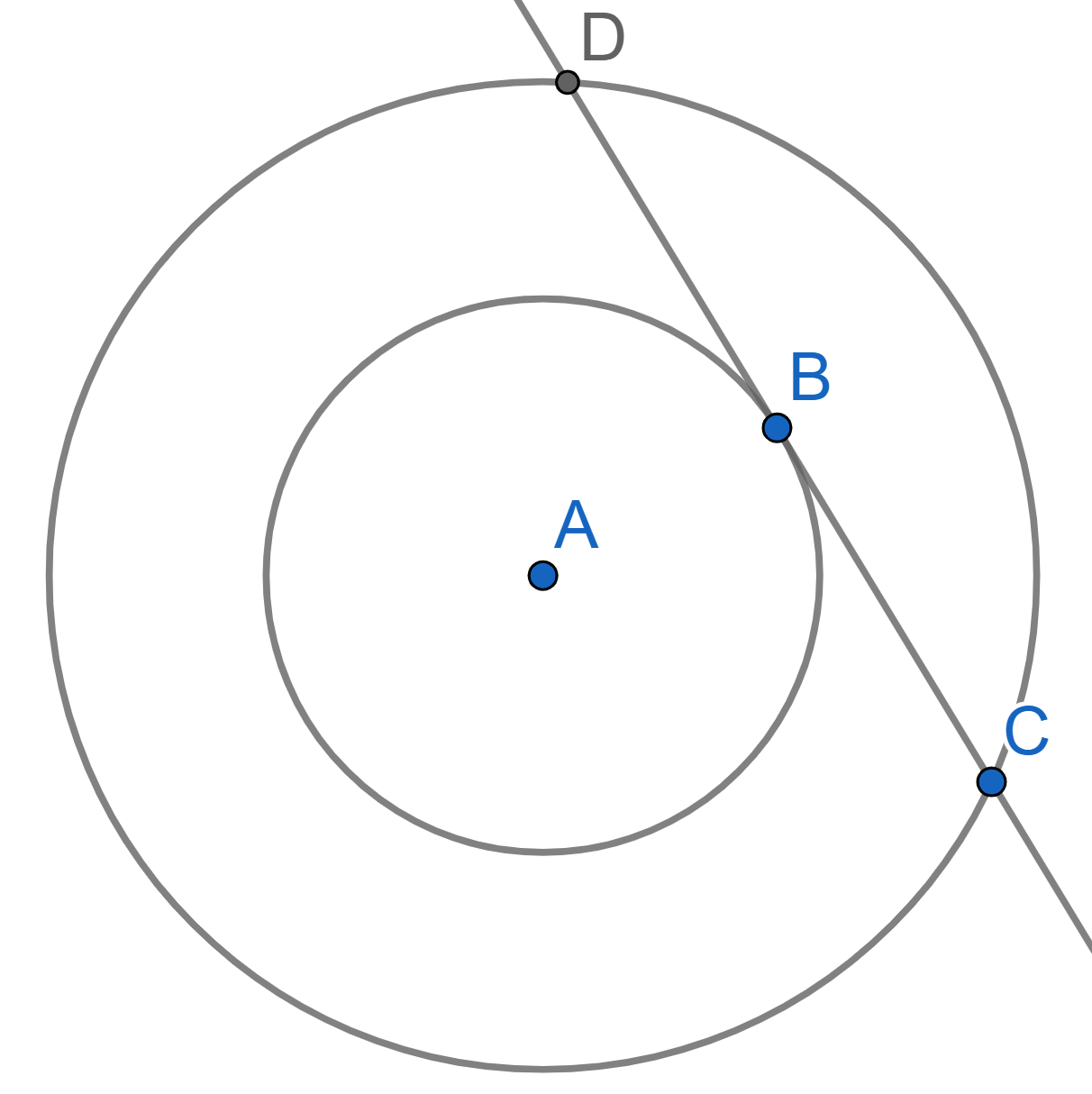
Take two circles with a common centre \(A\). A chord \(CD\) of the bigger circle is tangent to the smaller one at the point \(B\). Prove that \(B\) is the midpoint of \(CD\).
Prove that the lines tangent to a circle in two opposite points of a diameter are parallel.
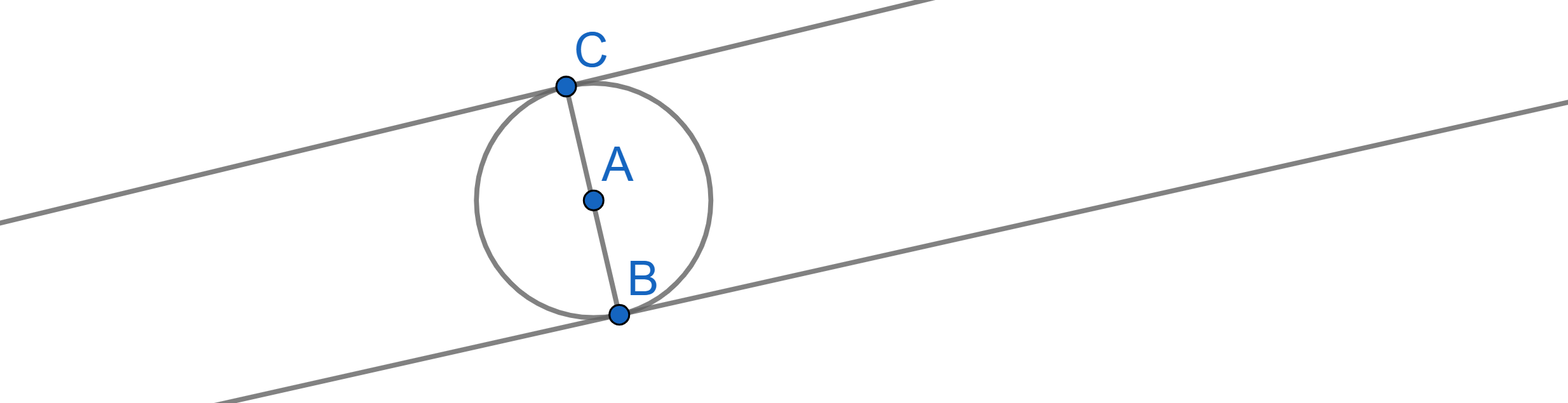
\(CD\) is a chord of a circle with centre \(A\). The line \(CD\) is parallel to the tangent to the circle at the point \(B\). Prove that the triangle \(BCD\) is isosceles.
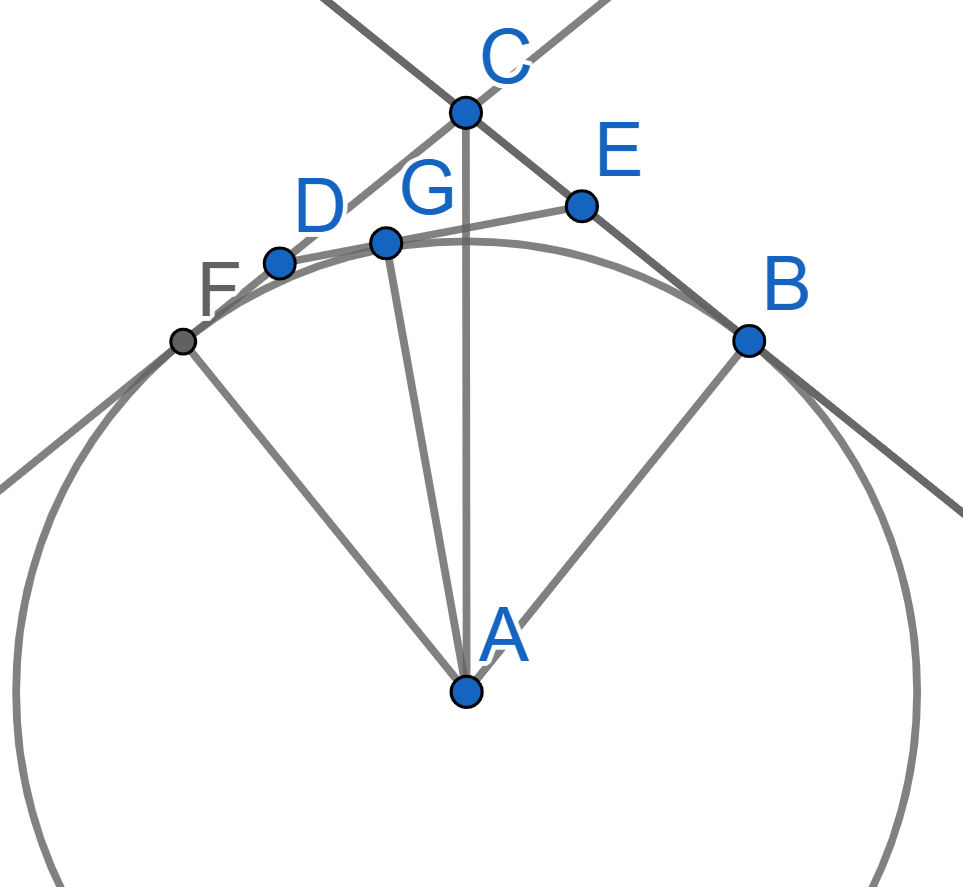
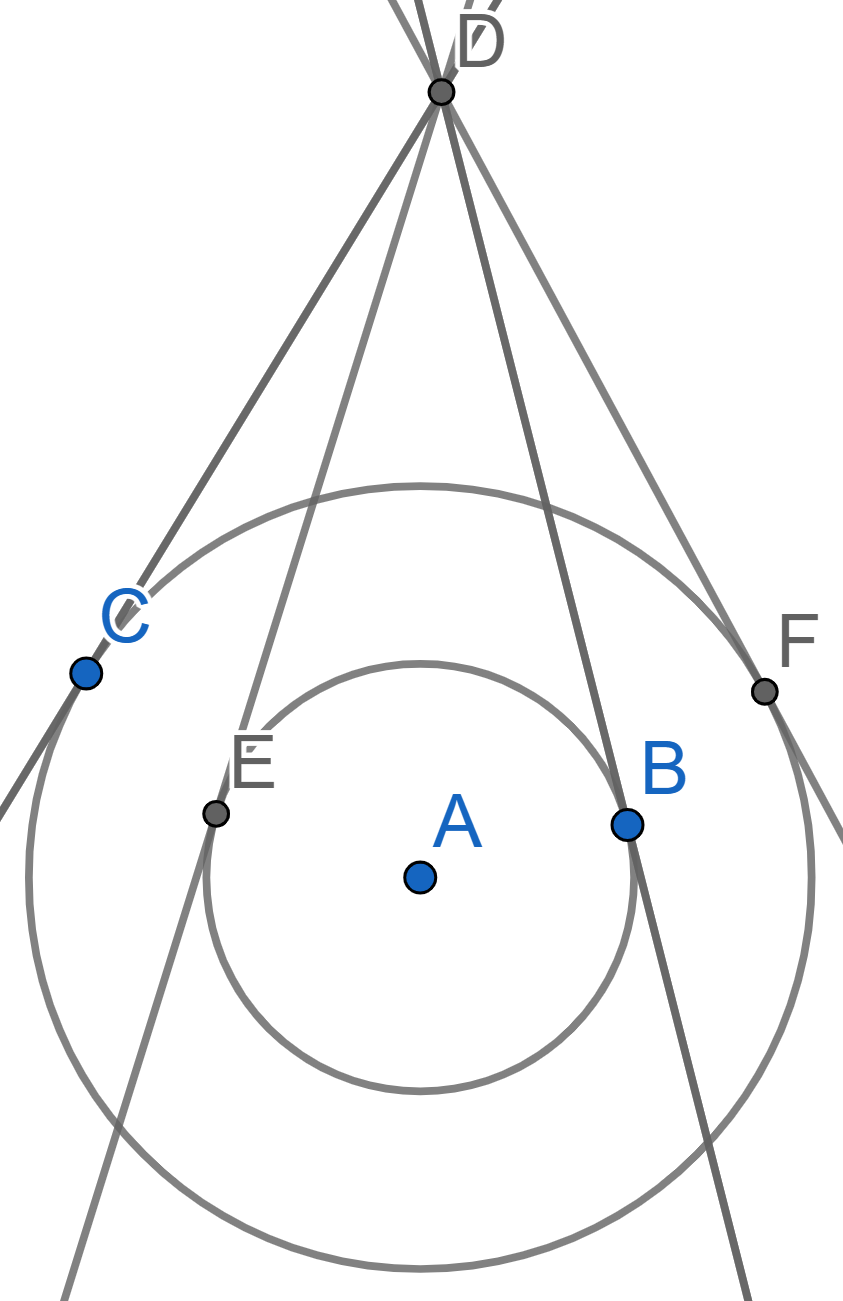
Four lines, intersecting at the point \(D\), are tangent to two circles with a common center \(A\) at the points \(C,F\) and \(B,E\). Prove that there exists a circle passing through all the points \(A,B,C,D,E,F\).
A circle with center \(A\) is inscribed into the triangle \(CDE\), so that all the sides of the triangle are tangent to the circle. We know the lengths of the segments \(ED=c, CD=a, EC=b\). The line \(CD\) is tangent to the circle at the point \(B\) - find the lengths of segments \(BD\) and \(BC\).
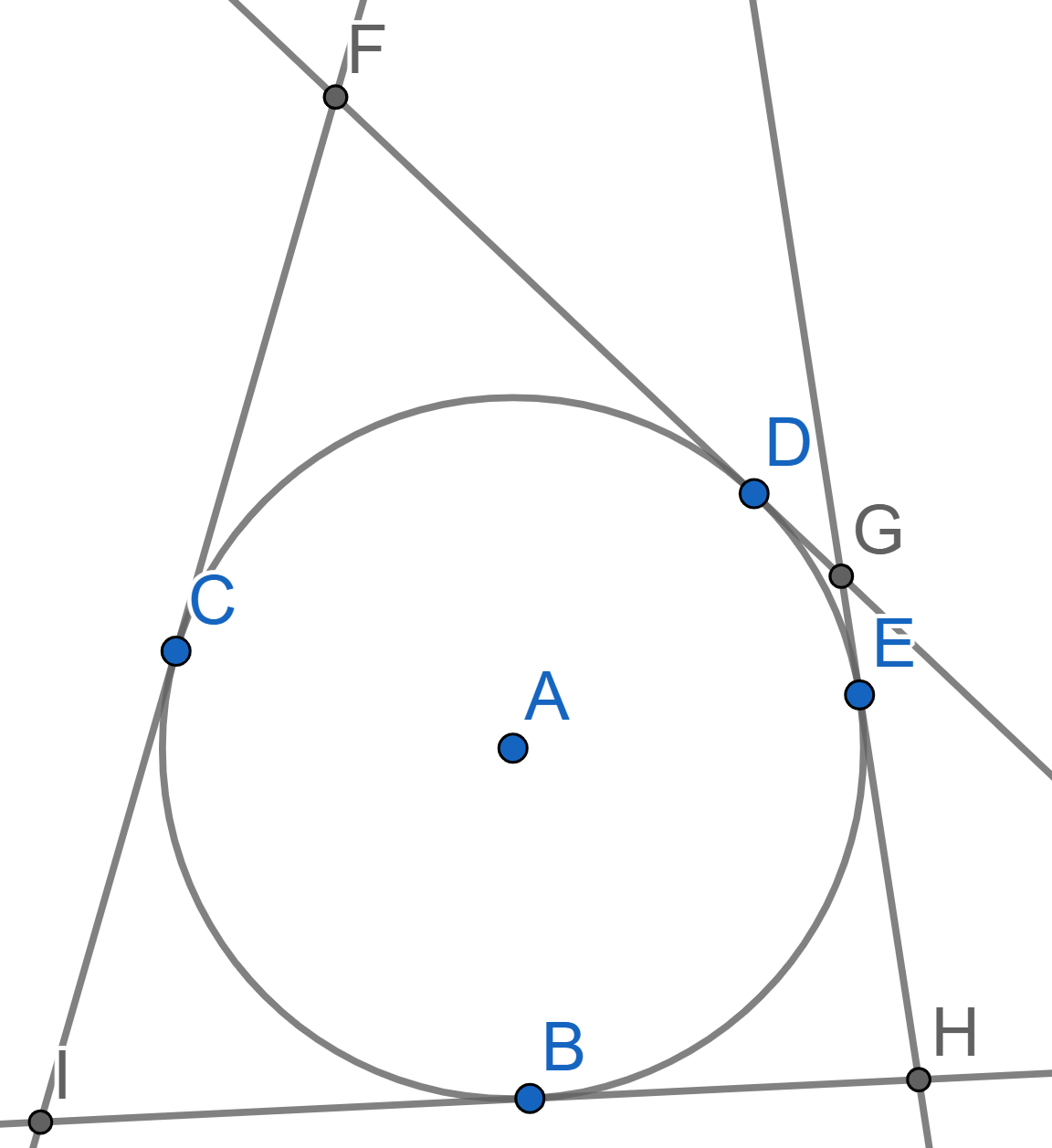
A circle with center \(A\) is tangent to all the sides of the quadrilateral \(FGHI\) at the points \(B,C,D,E\). Prove that \(FG+HI = GH+FI\).
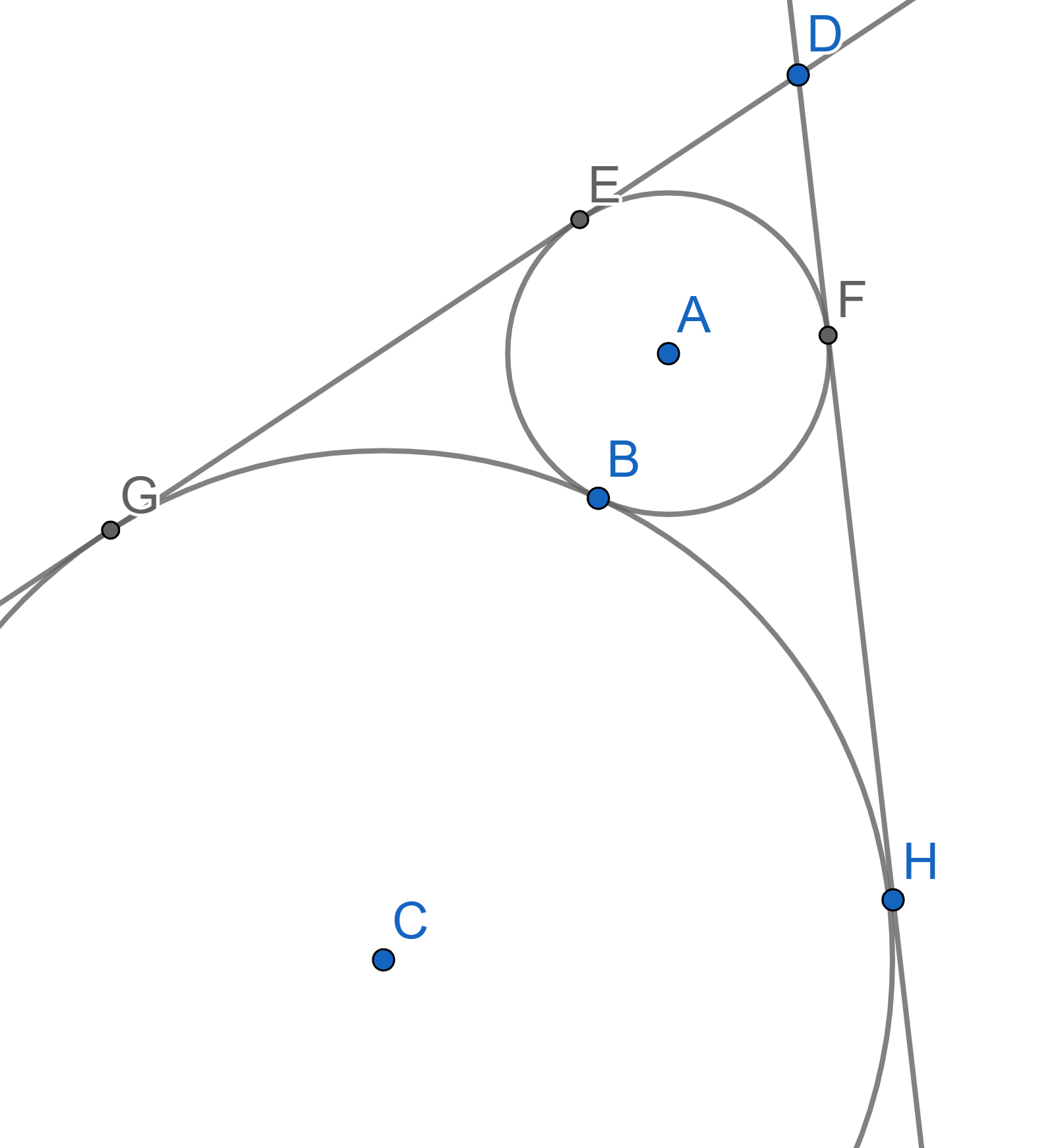
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Both circles are tangent to the sides of an angle with vertex \(D\). It is known that the angle \(\angle EDF = 60^{\circ}\) and the radius of the smaller circle \(AF=5\). Find the radius of the large circle.