Problems

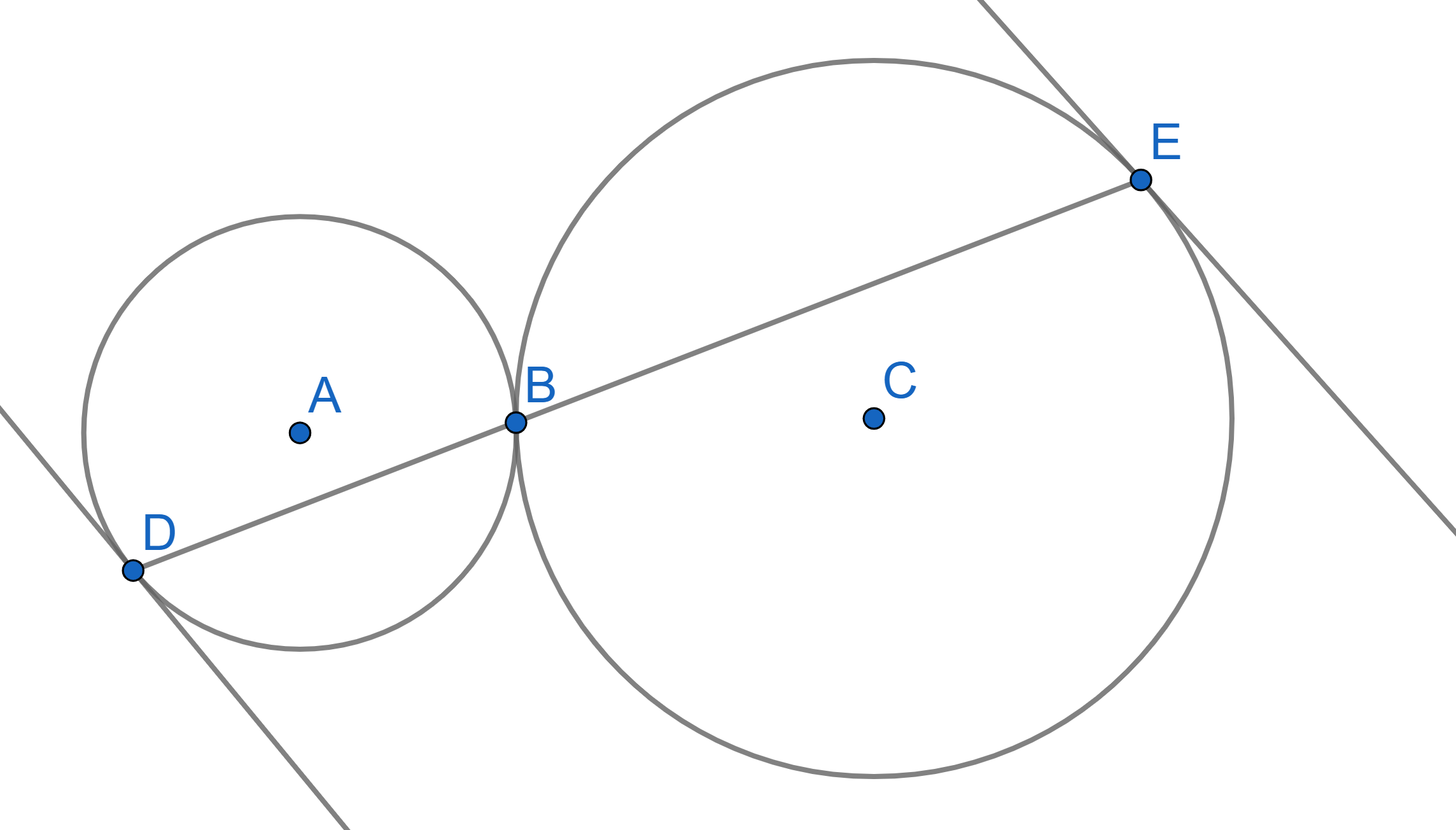
Two circles with centres \(A\) and \(C\) are tangent to each other at the point \(B\). Two points \(D\) and \(E\) are chosen on the circles in such a way that a segment \(DE\) passes through the point \(B\). Prove that the tangent line to one circle at the point \(D\) is parallel to the tangent line to the other circle at the point \(E\).

Is it true that if \(a\) is a positive number, then \(a^2 \ge a\)? What about \(a^2 +1 \ge a\)?

Show for positive \(a\) and \(b\) that \(a^2 +b^2 \ge 2ab\).

Is it true that if \(b\) is a positive number, then \(b^3 + b^2 \ge b\)? What about \(b^3 +1 \ge b\)?

Show that if \(a\) is positive, then \(1+a \ge 2 \sqrt{a}\).

Let \(k\) be a natural number, prove the following inequality. \[\frac1{k^2} > \frac1{k} - \frac1{k+1}.\]

Show that if \(a\) is a positive number, then \(a^3+2 \ge 2a \sqrt{a}\).

The numbers \(a\), \(b\) and \(c\) are positive. By completing the square, show that \[\frac{a^2}4 + b^2 + c^2 \ge ab-ac+2bc.\]

Let \(m\) and \(n\) be natural numbers such that \(m>n\). Show that: \[\frac1{n^2} + \frac1{(n+1)^2} + \frac1{(n+2)^2} + \dots + \frac1{m^2} > \frac1{n} - \frac1{m}.\]

The numbers \(a,b,c\) are positive. Show that: \[\frac{ab}{c} + \frac{bc}{a} + \frac{ac}{b} \ge a +b+c.\]