Problems
The natural numbers \(a,b,c,d\) are such that \(ab=cd\). Prove that the number \(a^{2025} + b^{2025} + c^{2025} + d^{2025}\) is composite.
Prove that for an arbitrary odd \(n = 2m - 1\) the sum \(S = 1^n + 2^n + ... + n^n\) is divisible by \(1 + 2 + ... + n = nm\).
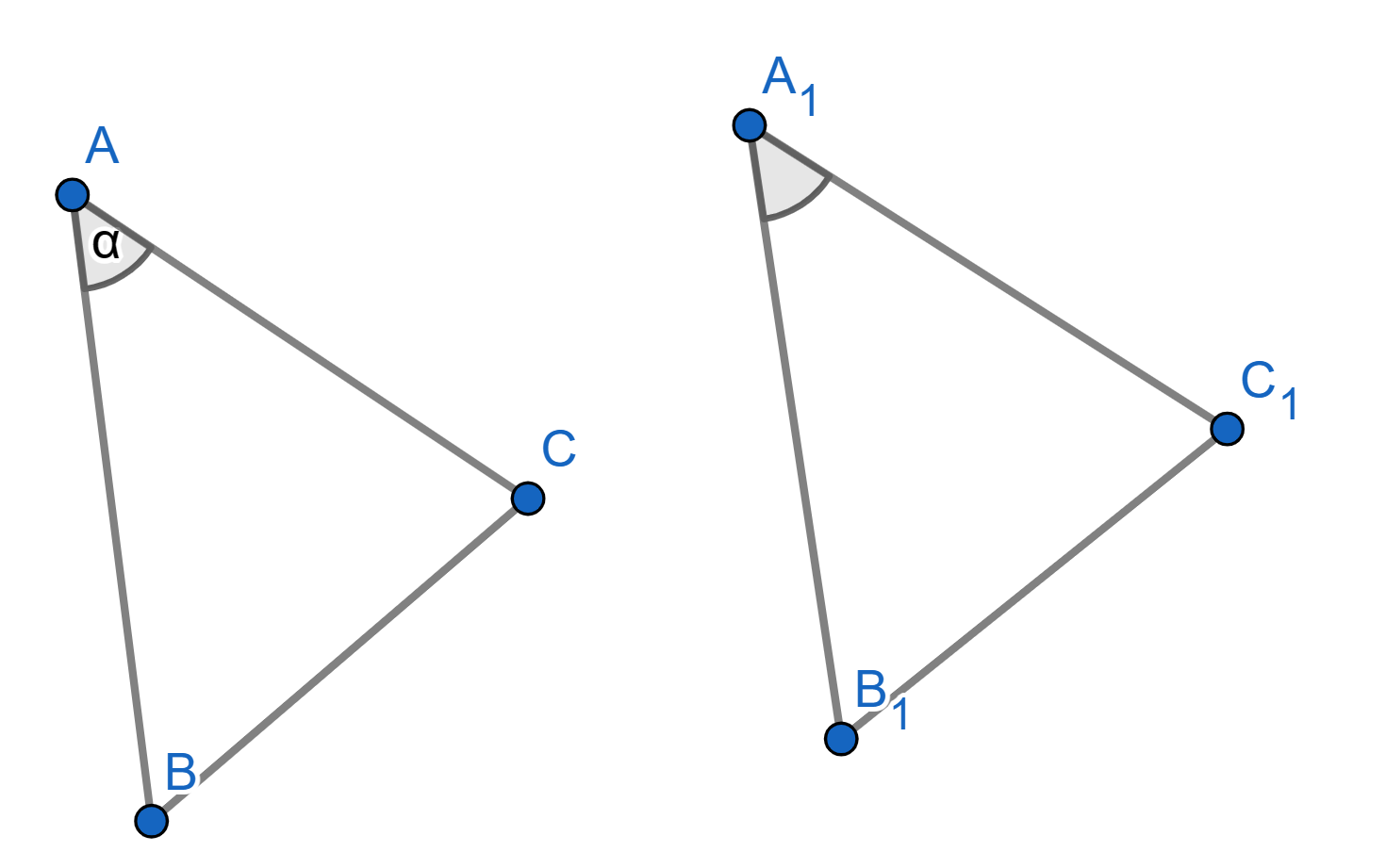
Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.
In the triangle \(\triangle ABC\) the sides \(AC\) and \(BC\) are equal. Prove that the angles \(\angle CAB\) and \(\angle CBA\) are equal.
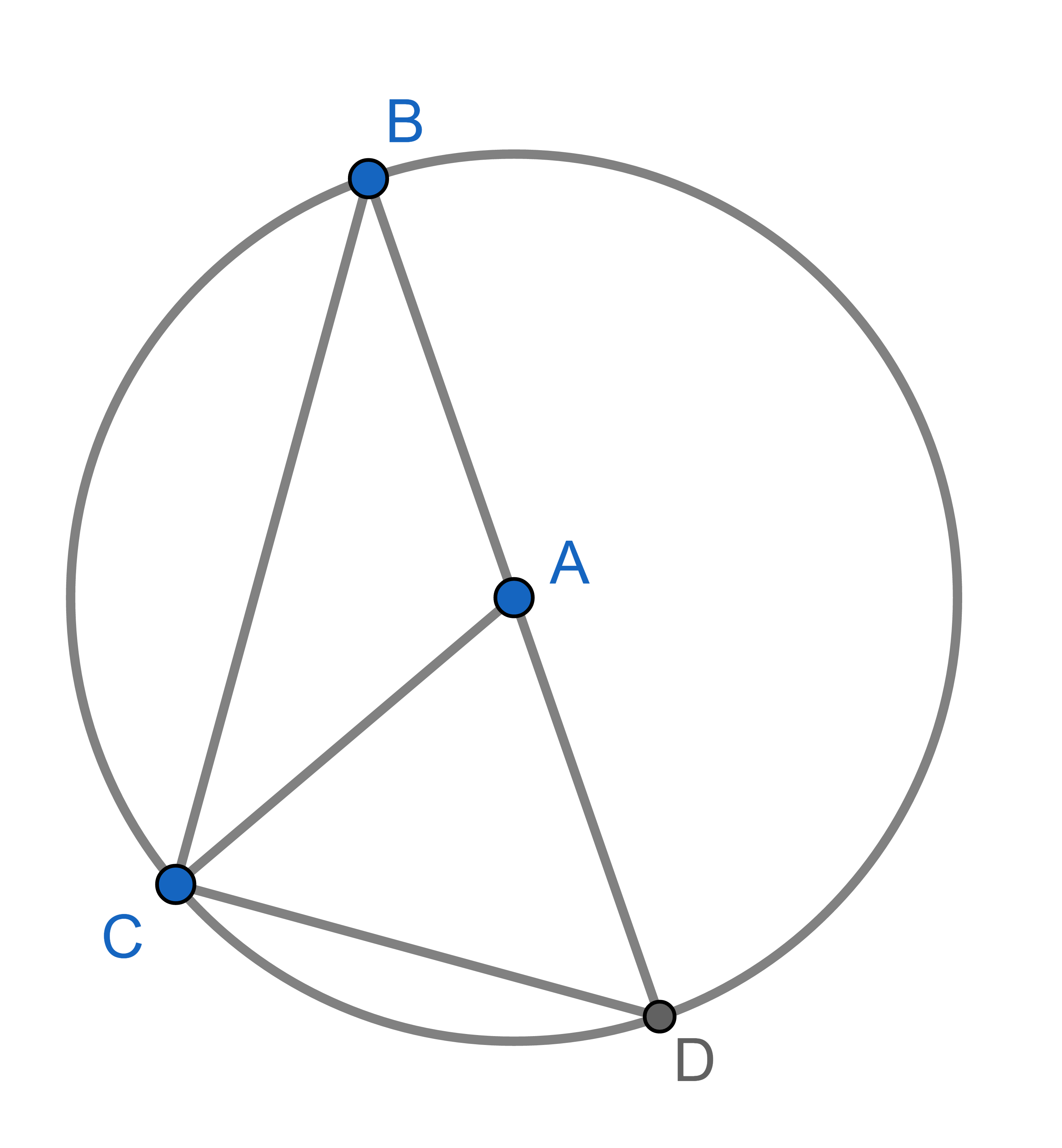
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. The segment \(BD\) is a diameter of the circle. Show that \(\angle CAD = 2 \angle CBD\). This is a special case of the inscribed angle theorem.
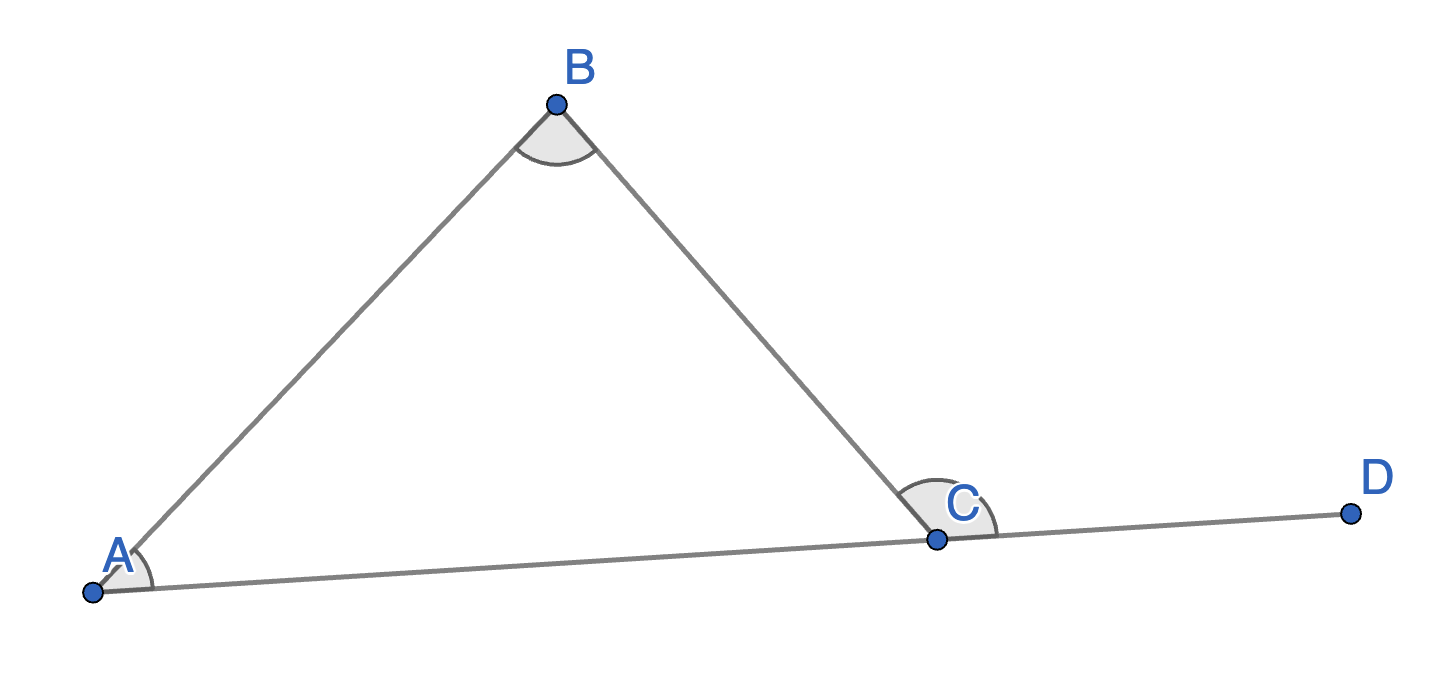
Let \(ABC\) be a triangle with given angles \(\angle BAC\) and \(\angle ABC\). What is the value of the angle \(\angle BCD\) in terms of \(\angle BAC\) and \(\angle ABC\)?
Point \(A\) is the centre of a circle and points \(B,C,D\) lie on that circle. Show that \(\angle CAD = 2 \angle CBD\). This statement is known as the inscribed angle theorem and is used widely in Euclidean geometry.
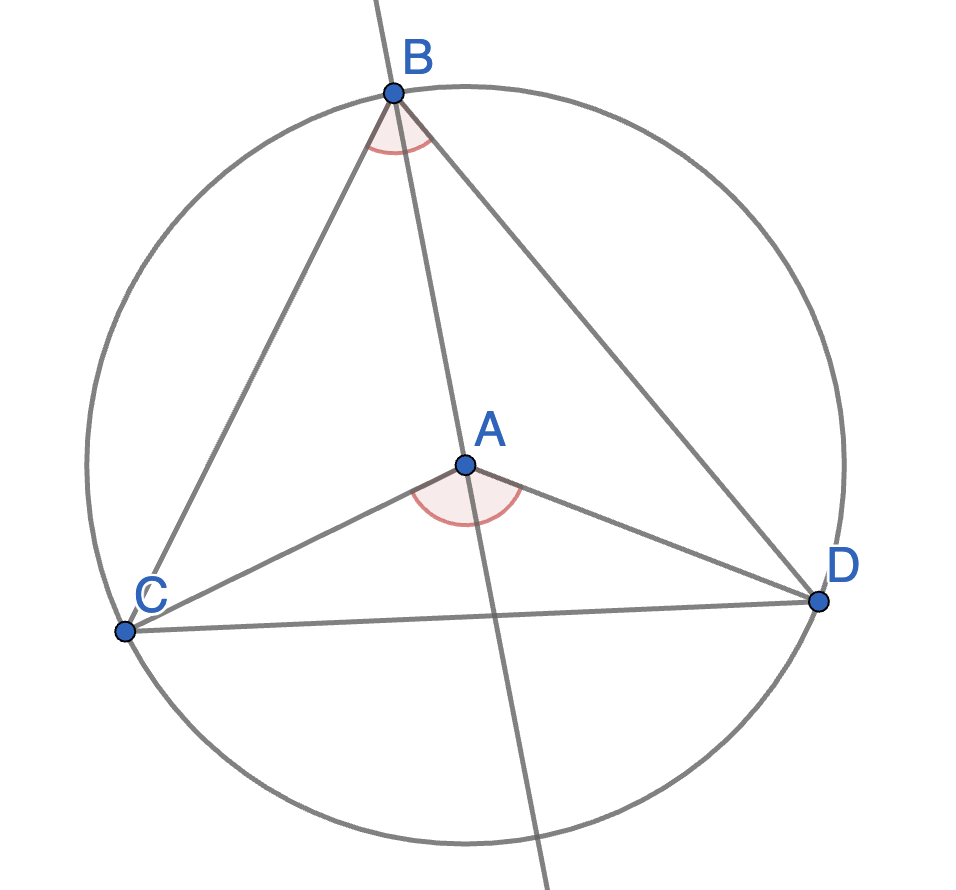
Let \(BCDE\) be a quadrilateral inscribed in a circle with centre \(A\). Show that angles \(\angle CDE\) and \(\angle CBE\) are equal. Also show that angles \(\angle BCD\) and \(\angle BED\) are equal. This says that all angles at the circumference subtended by the same arc are equal.
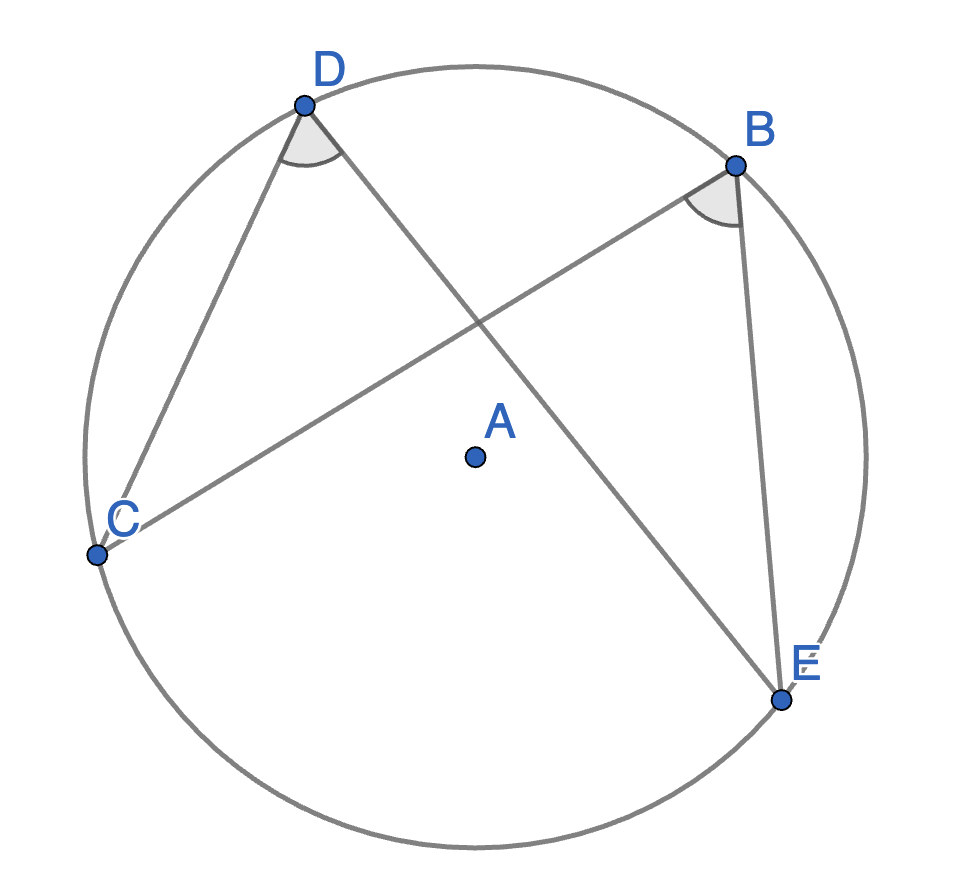
Let \(BCDE\) be an inscribed quadrilateral. Show that \(\angle BCD + \angle BED = 180^{\circ}\).
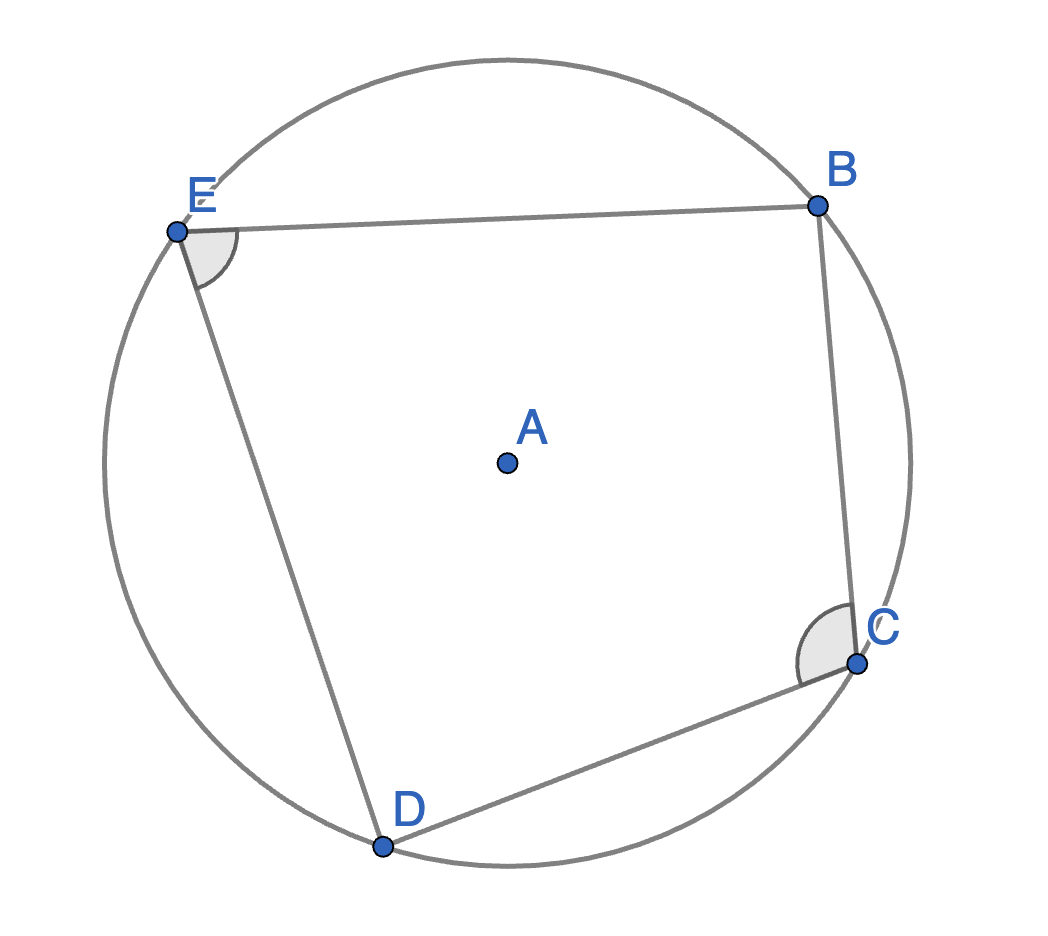
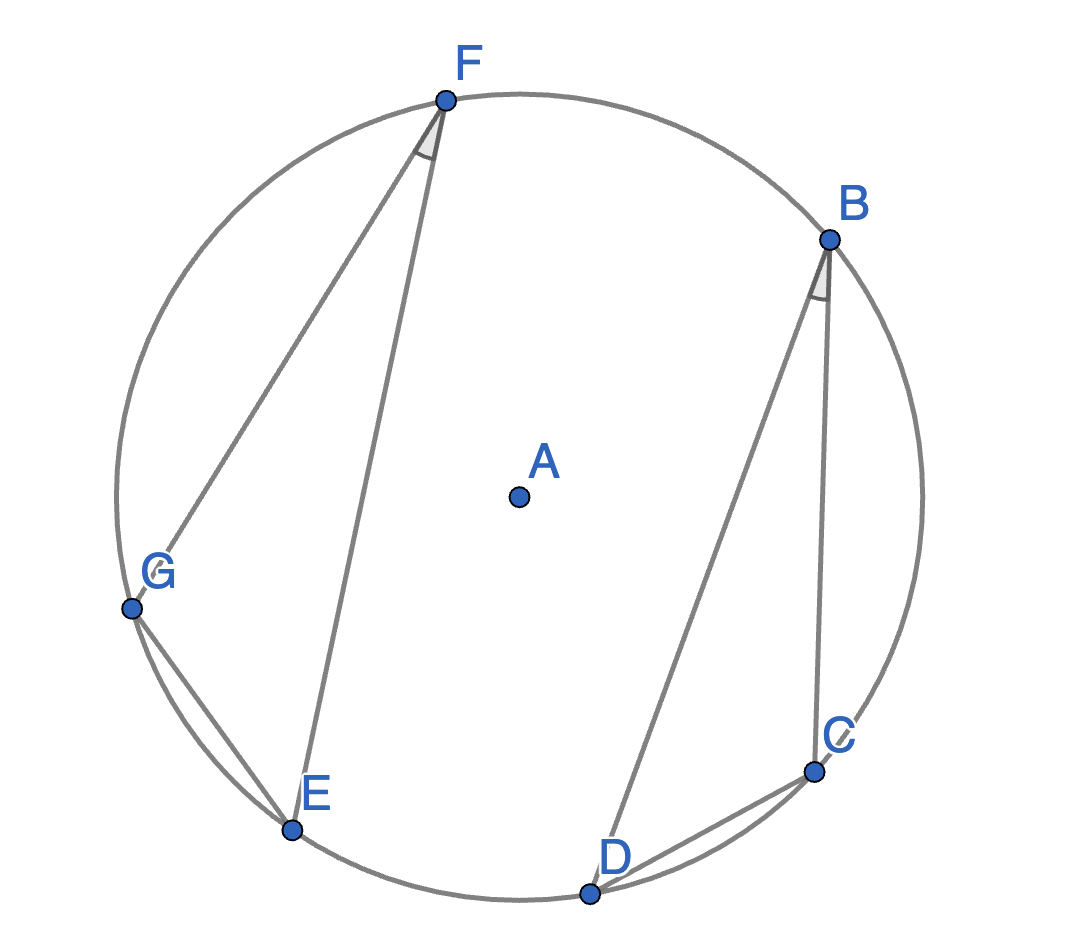
The points \(B\),\(C\),\(D\),\(E\),\(F\) and \(G\) lie on a circle with centre \(A\). The angles \(\angle CBD\) and \(\angle EFG\) are equal. Prove that the segments \(CD\) and \(EG\) have equal lengths.