Problems
In a tournament, 100 wrestlers are taking part, all of whom have different strengths. In any fight between two wrestlers, the one who is stronger always wins. In the first round the wrestlers broke into random pairs and fought each other. For the second round, the wrestlers once again broke into random pairs of rivals (it could be that some pairs will repeat). The prize is given to those who win both matches. Find:
a) the smallest possible number of tournament winners;
b) the mathematical expectation of the number of tournament winners.
Four outwardly identical coins weigh 1, 2, 3 and 4 grams respectively.
Is it possible to find out in four weighings on a set of scales without weights, which one weighs how much?
In each cell of a board of size \(5\times5\) a cross or a nought is placed, and no three crosses are positioned in a row, either horizontally, vertically or diagonally. What is the largest number of crosses on the board?
An after school club is attended by 4 boys from class 7A, and four from class 7B. Of those who attended three were named Ben, three were named Will, and two were named Tom.
Is it possible for it to be the case that each boy had at least one namesake classmate who attended the club?
Authors: B. Vysokanov, N. Medved, V. Bragin
The teacher grades tests on a scale from 0 to 100. The school can change the upper bound of the scale to any other natural number, recalculating the estimates proportionally and rounding up to integers. A non-integer number, when rounded, changes to the nearest integer; if the fractional part is equal to 0.5, the direction of rounding can be either up or down and it can be different for each question. (For example, an estimate of 37 on a scale of 100 after recalculation in the scale of 40 will go to \(37 \cdot 40/100 = 14.8\) and will be rounded to 15).
The students of Peter and Valerie got marks, which are not 0 and 100. Prove that the school can do several conversions so that Peter’s mark becomes b and Valerie’s mark becomes a (both marks are recalculated simultaneously).
There was a football match of 10 versus 10 players between a team of liars (who always lie) and a team of truth-tellers (who always tell the truth). After the match, each player was asked: “How many goals did you score?” Some participants answered “one”, Callum said “two”, some answered “three”, and the rest said “five”. Is Callum lying if it is known that the truth-tellers won with a score of 20:17?
Out of the given numbers 1, 2, 3, ..., 1000, find the largest number \(m\) that has this property: no matter which \(m\) of these numbers you delete, among the remaining \(1000 - m\) numbers there are two, of which one is divisible by the other.
Author: A.A. Egorov
Calculate the square root of the number \(0.111 \dots 111\) (100 ones) to within a) 100; b) 101; c)* 200 decimal places.
A rectangular chocolate bar size \(5 \times 10\) is divided by vertical and horizontal division lines into 50 square pieces. Two players are playing the following game. The one who starts breaks the chocolate bar along some division line into two rectangular pieces and puts the resulting pieces on the table. Then players take turns doing the same operation: each time the player whose turn it is at the moment breaks one of the parts into two parts. The one who is the first to break off a square slice \(1\times 1\) (without division lines) a) loses; b) wins. Which of the players can secure a win: the one who starts or the other one?
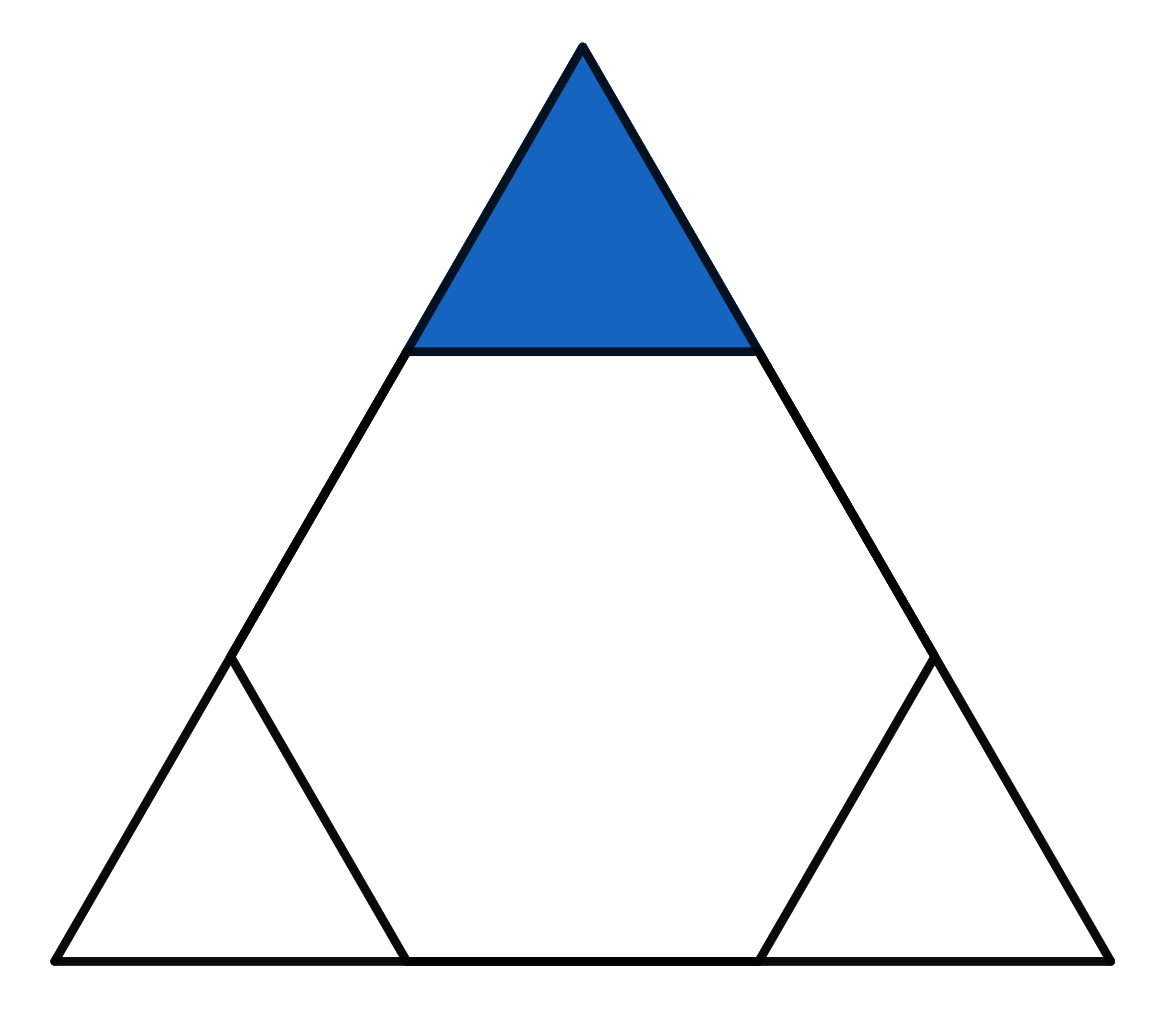
The triangle visible in the picture is equilateral. The hexagon inside is a regular hexagon. If the area of the whole big triangle is \(18\), find the area of the small blue triangle.