Problems

Now let’s imagine a \(3\times 3\) board, how can you turn on just the middle light?

A very important tool in maths is to use symmetries to make problems easier. A symmetry of a shape is a movement that leaves it looking exactly the same. For example, rotating a square by \(90^\circ\) (spinning it by a quarter turn) is a symmetry. Imagine you are playing lights out on a board that has no quiet plans. Explain why if a light pattern has a certain symmetry, then its corresponding plan will also have the same symmetry.

A \(3\times 3\) “Lights Out" board starts being all off. Explain why \(5\) is the smallest number of presses you need to turn the whole board on.

Imagine a “Lights Out” board that starts with all the lights off. A plan that is not empty (it has at least one button in it) is called quiet if, after pressing all the buttons in the plan, the board ends up all off again (remember that plans can’t have buttons being pressed twice). Now take a \(3\times 2\) “Lights Out” board. Can you find two different ways to turn every light on? How can this help you to discover a quiet plan?

Let’s now play with the \(2\times 3\) “Lights Out’’ board. You can take it as a fact that there are exactly \(3\) quiet plans for this board (you can read example \(3\) again to remind yourself of quiet plans). Can you find them all? Using this, or otherwise, can you work \(4\) plans that produce the following pattern?

Below you see three light patterns and their matching plans. Each plan turns all lights on except one square: the centre, the top-left corner, or the top-middle light. Explain why, using these plans, and one fourth plan that you need to find, any light pattern on the \(3\times3\) board can be made by a suitable plan.

Alice and Jamie each have an identical “Lights Out” board (same size, same rules). Both boards start with all lights off, and on this board size there are no quiet plans. Alice presses a plan \(A\); Jamie presses a different plan \(B\) (not the same set of buttons). Could they end up with exactly the same final pattern of lights?

On a \(5\times5\) “Lights Out” board, it turns out that there is a simple rule to turn the whole board off regardless of which lights are on at the start:

1. Chase down. Start at the top row. For each light in that row that is turned on, press the button directly below it so that it turns off. Move to the next row and repeat. This turns off rows one by one; only the bottom row may be left with lights being on.

2. Fix the bottom. Find your bottom row in the table and press on the top row the pattern shown to the right. Then chase down again. Repeat until everything is off.

Can you explain why this works?

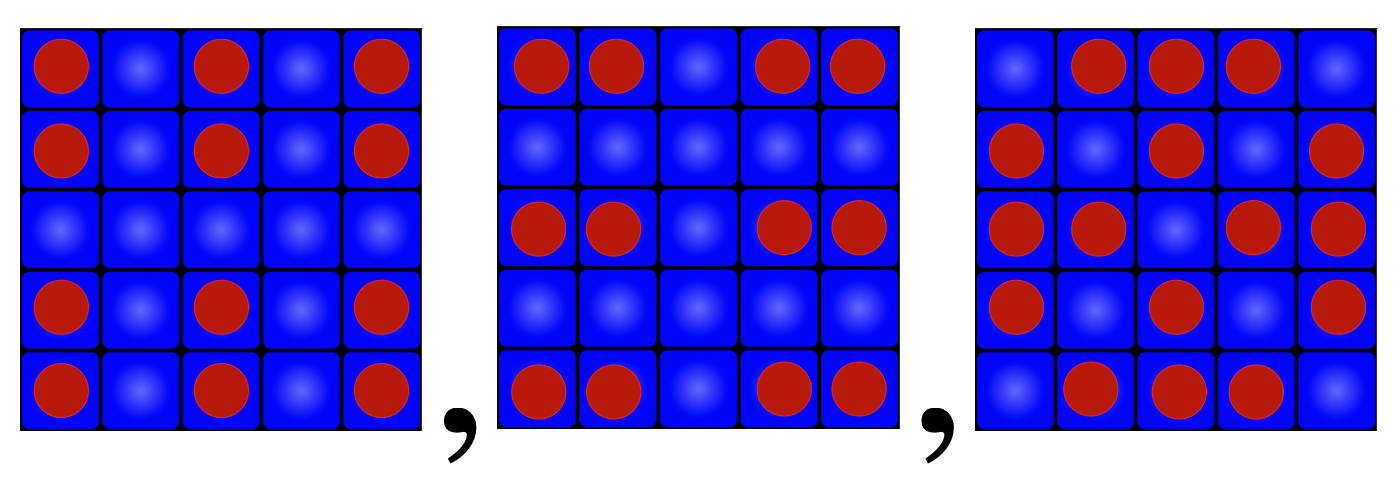
George is playing on the \(5\times 5\) “Lights Out" board and says that since each light can be on or off, and there are \(25\) lights on the board, the number possible light patterns that can be achieved by playing the game is \(2^{25}\). It turns out that the number is much smaller, it is \(2^{23}\). Can you explain why? You may take it as a fact that these three are the only quiet plans of the \(5\times 5\) board: