Problems
Show that \(R(4,4)\le18\) - that is, no matter how you colour the edges of \(K_{18}\), there must be a monochromatic \(K_4\).
By considering \(k-1\) copies of \(K_{k-1}\), show that \(R(k,k)\ge(k-1)^2\).
Let \(s>2\) and \(t>2\) be integers. Show that \(R(s,t)\le R(s-1,t)+R(s,t-1)\).
Using \(R(s,t)\le R(s-1,t)+R(s,t-1)\), prove that \(R(k,k)\le 4^k\).
Explain why you can’t rotate the sides on a normal Rubik’s cube to get to the following picture (with no removing stickers, painting, or other cheating allowed).

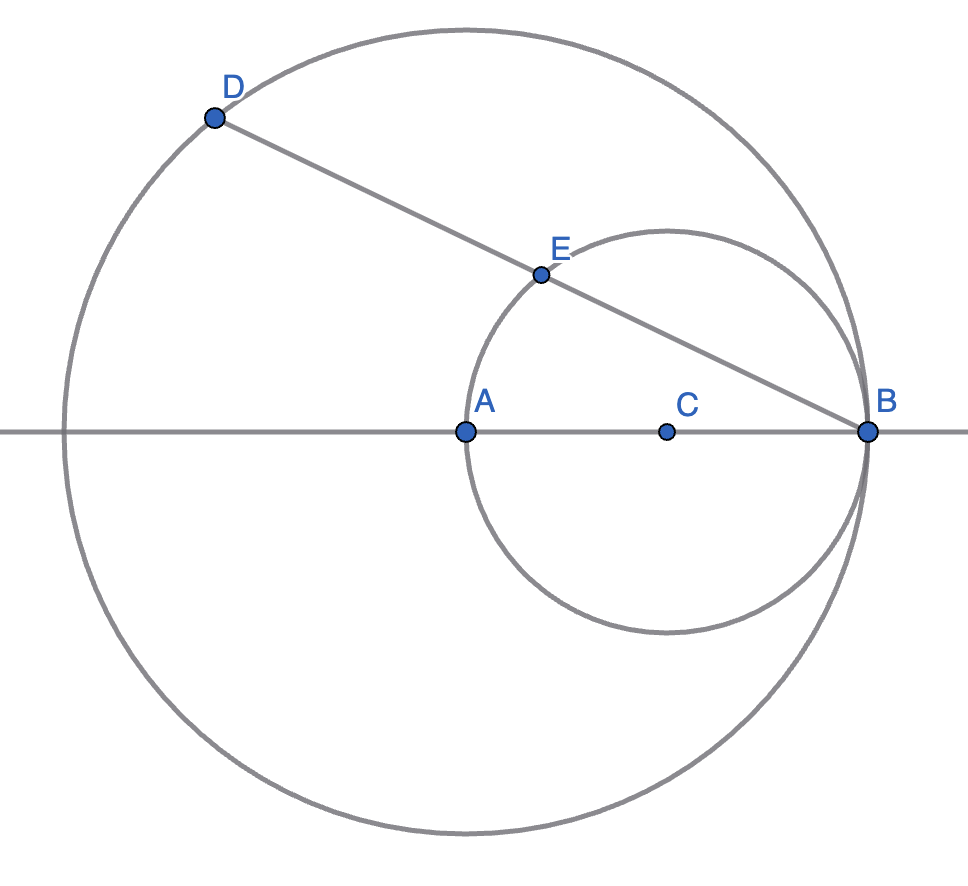
A circle with centre \(A\) has the point \(B\) on its circumference. A smaller circle is drawn inside this with \(AB\) as a diameter and \(C\) as its centre. A point \(D\) (which is not \(B\)) is chosen on the circumference of the bigger circle, and the line \(BD\) is drawn. \(E\) is the point where the line \(BD\) intersects the smaller circle.
Show that \(|BE|=|DE|\).
Are there any two-digit numbers which are the product of their digits?
The sum of Matt’s and Parker’s ages is \(63\) years. Matt is twice as old as Parker was when Matt was as old as Parker is now. How old are they? (Show that there’s no other ages that they could have)
How many \(10\)-digit numbers are there such that the sum of their digits is \(3\)?