Problems

Elections are approaching in Problemland! There are three candidates for president: \(A\), \(B\), and \(C\).

An opinion poll reports that \(65\%\) of voters would be satisfied with \(A\), \(57\%\) with \(B\), and \(58\%\) with \(C\). It also says that \(28\%\) would accept \(A\) or \(B\), \(30\%\) \(A\) or \(C\), \(27\%\) \(B\) or \(C\), and that \(12\%\) would be content with all three candidates.

Show that there must have been a mistake in the poll.

You are creating passwords of length \(8\) using only the letters \(A\), \(B\), and \(C\). Each password must use all three letters at least once.

How many such passwords are there?

How many numbers from \(1\) to \(1000\) are divisible by \(2\) or \(3\)?

The inclusion-exclusion principle is an immensely useful counting tool. This stems from the intuitive idea of overcounting and undercounting.

Suppose there are two properties \(A\) and \(B\) that some objects may or may not satisfy. Let us say that there are \(a\) objects with property \(A\) and \(b\) objects with property \(B\). We can ask, “how many objects have at least one of the two properties?"

If the objects can have either property \(A\) or \(B\), but not both, then \(a+b\) is correct count. However, if objects can have both property \(A\) and \(B\), then \(a+b\) counts those with both properties twice. In the picture below, objects are represented as red dots and the number indicate how many times we have counted the objects in that region.

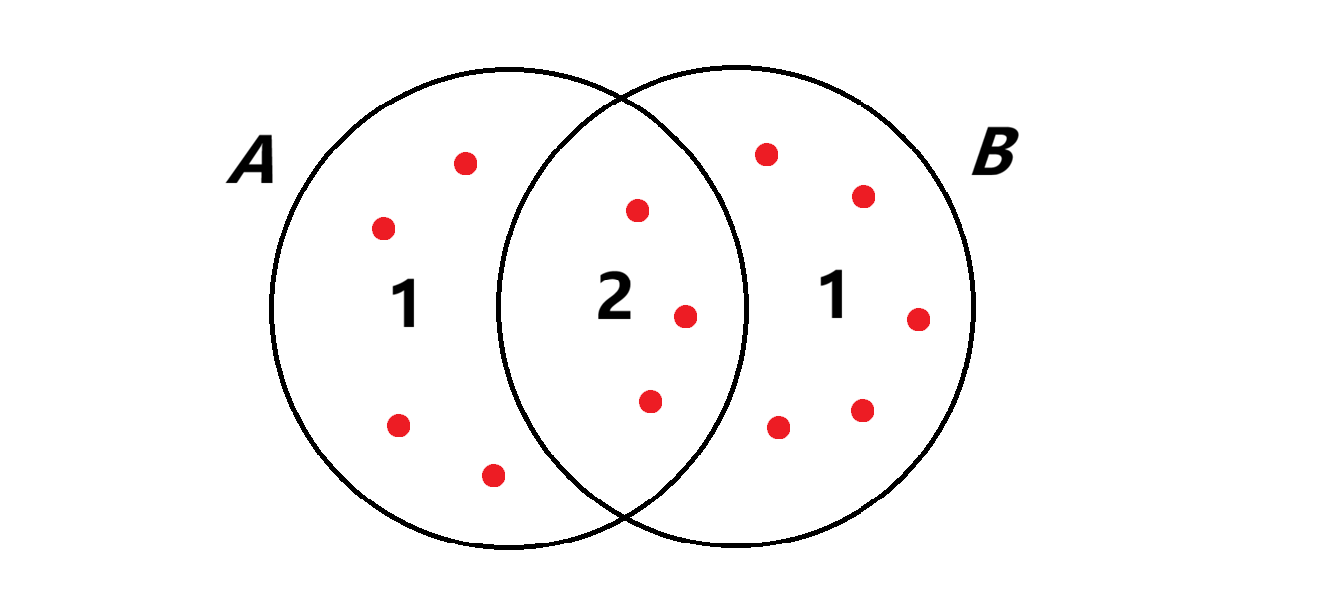
Let the number of objects having both properties be \(x\). Here we are clearly counting these object twice. To get the correct count, we need subtract \(x\). So the total number should be \(a+b-x\).

Let us also think about what may have if we have three properties \(A,B,C\). Let us say that there are \(a\) objects with property \(A\), \(b\) objects with property \(B\) and \(c\) objects with property \(C\). The number \(a+b+c\) again overcounts. By how much? Drawing a cartoon picture is again helpful.

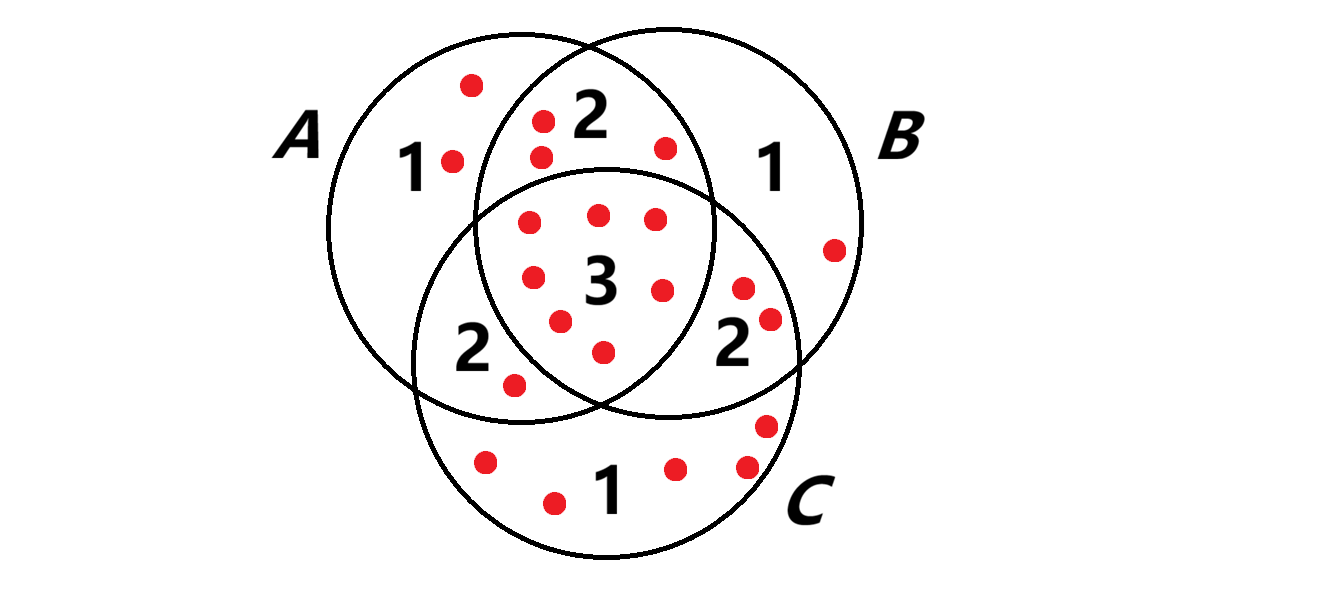
Let \(x\) be the number of objects with property \(A\) and \(B\), \(y\) the number of objects with property \(B\) and \(C\), \(z\) the number of objects with property \(A\) and \(C\). As before, we want to subtract \(x\) to correct for the number of objects with property \(A\) and \(B\). Similarly, we should subtract \(y\) and \(z\). So is \(a+b+c-x-y-z\) the correct count?

Here run into the opposite problem. We are not counting the number of objects with all three properties. Here is a cartoon for \(a+b+c-x-y-z\):

Let \(w\) be the number of objects with all three properties. The correct count is \(a+b+c-x-y-z+w\).

Of course, we do not have to stop at three properties! However, the formulas become longer to write down. The important part is to understand when you are overcounting or undercounting and how to correct for them. For the moment, let us have a look at some examples, which should make the reasoning and formula easier to digest.

Three kinds of cookies are sold at a store: dark chocolate \((D)\), raspberry with white chocolate \((R)\) and honeycomb \((H)\). Here is a table summarizing the number of people buying cookies this morning.

The column with label \(D,H\), for example, means the the number of people who bought both dark chocolate and honeycomb cookies.

How many people bought cookies this morning?