Problems
You have 26 constants, labeled \(A\) through \(Z\). Let \(A\) equal 1. The other constants have values equal to the letter’s position in the alphabet, raised to the power of the previous constant. That means that \(B\) (the second letter) = \(2^A=2^1= 2\), \(C = 3^B=3^2= 9\), and so on. Find the exact numerical value for this expression: \[(X-A)(X-B)(X-C)\dots (X-Y)(X-Z).\]
Why does a mirror reverse right and left instead of up and down?
After removing a \(1\times 1\) square from the corner of a \(4\times 4\) square, we are left with the following shape:
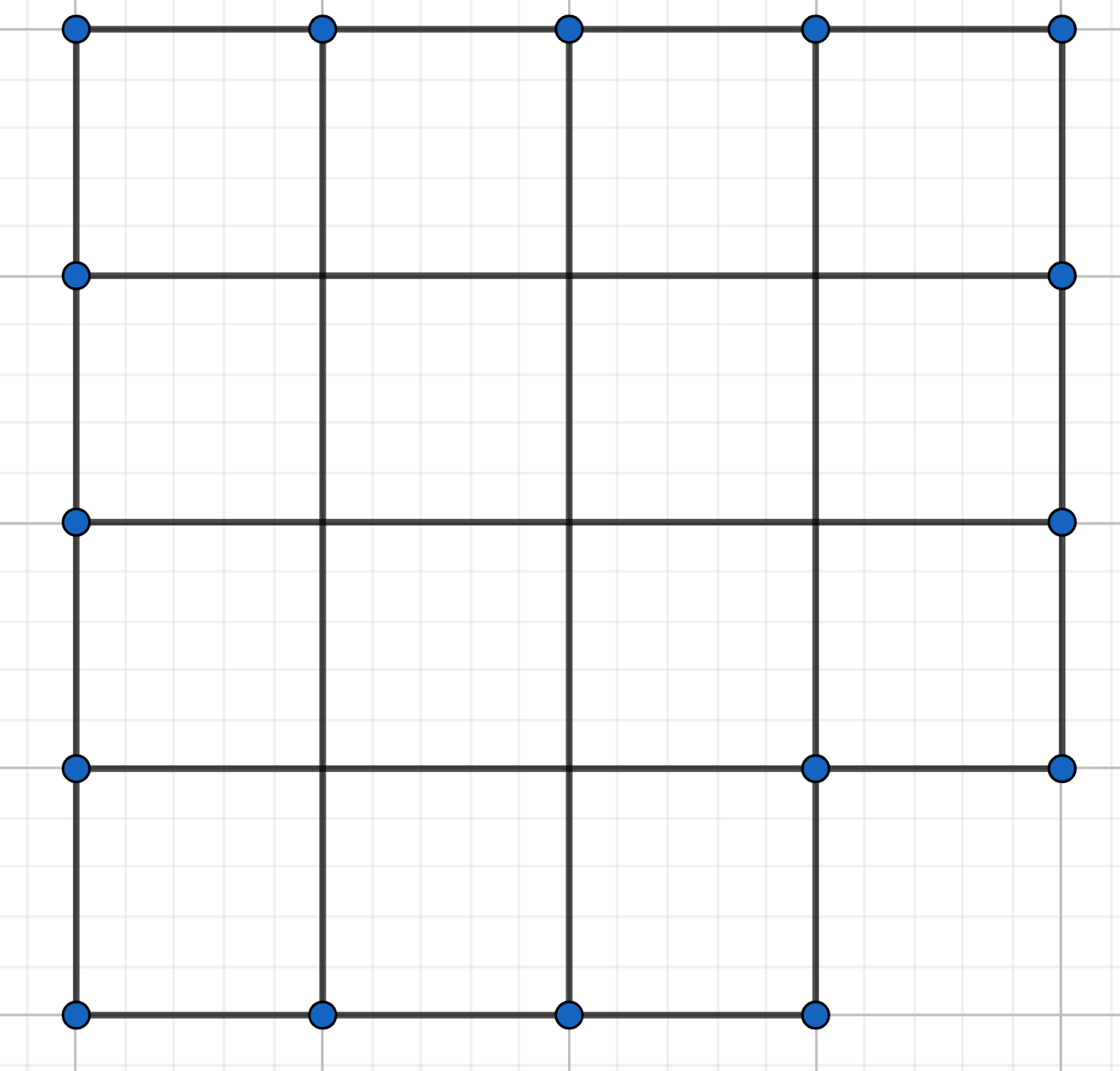
how can we cut this into three congruent shapes?
Max asked Emily how old she was. She replied that she was 13 years old the day before yesterday, and will be 16 next year. Then, Max asked her brother, whether it was true, and he said yes. How is it possible if nobody was lying?
The date 21.02.2012 reads the same forwards and backwords (such numbers are called palindromes). Are there any more palindrome dates in the twenty first centuary?
Do there exist three natural numbers such that neither of them divide each other, but each number divides the product of the other two?
Find all the solutions of the puzzle and prove there are no others. Different letters denote different digits, while the same letters correspond to the same digits. \[M+MEEE=BOOO.\]
Place coins on a \(6\times 6\) chequered board (one coin on one square), so that all the horizontal lines contain different number of coins, and all vertical lines contain the same number of coins.
Is it possible to arrange some group of distinct numbers in a circle so that each number equals the sum of its neighbours?
A big square was cut into smaller squares. Sebastian used all the pieces and constructed two squares with different side lengths by glueing the pieces together. Show an example of how he could do that.