Problems

There are ten islands in the Fantasia Archipelago. There used to be cruises connecting each island to each other island, each cruise served by a different ship. One day eight of those ships were taken over by pirates and do not serve cruises any more. Show that despite the efforts of pirates, it is still possible to get from each island to every other island, possibly changing ships on the way.

In Rabbitland you can get from any city to any other city. Bugs Bunny decided to find out what is the largest number of cities he can visit, while never visiting any city twice. He can start from any city and finish at any other. He realised that there are two longest paths he can take and they both involve the same number of cities. Show that those two paths have at least one city in common.

There are \(n\) people at a royal ball. Every time three of them meet and talk, it turns out some two of them didn’t know each other before. Show that the maximum number of connections between the guests is \(\frac14 n^2\). If any guest \(A\) knows guest \(B\), then \(B\) knows \(A\), and this counts as one connection.

An animal with \(n\) cells is a connected figure consisting of \(n\) equal-sized adjacent square cells. A dinosaur is an animal with at least 2007 cells. It is said to be primitive if its cells cannot be partitioned into two or more dinosaurs. Find with proof the maximum number of cells in a primitive dinosaur.

What time is it going to be in \(2025\) hours from now?

Prove that the product of five consecutive integers is divisible by \(30\).

Prove that if \(n\) is a composite number, then \(n\) is divisible by some natural number \(x\) such that \(1 < x\leq \sqrt{n}\).

The natural numbers \(a,b,c,d\) are such that \(ab=cd\). Prove that the number \(a^{2025} + b^{2025} + c^{2025} + d^{2025}\) is composite.

Prove that for an arbitrary odd \(n = 2m - 1\) the sum \(S = 1^n + 2^n + ... + n^n\) is divisible by \(1 + 2 + ... + n = nm\).

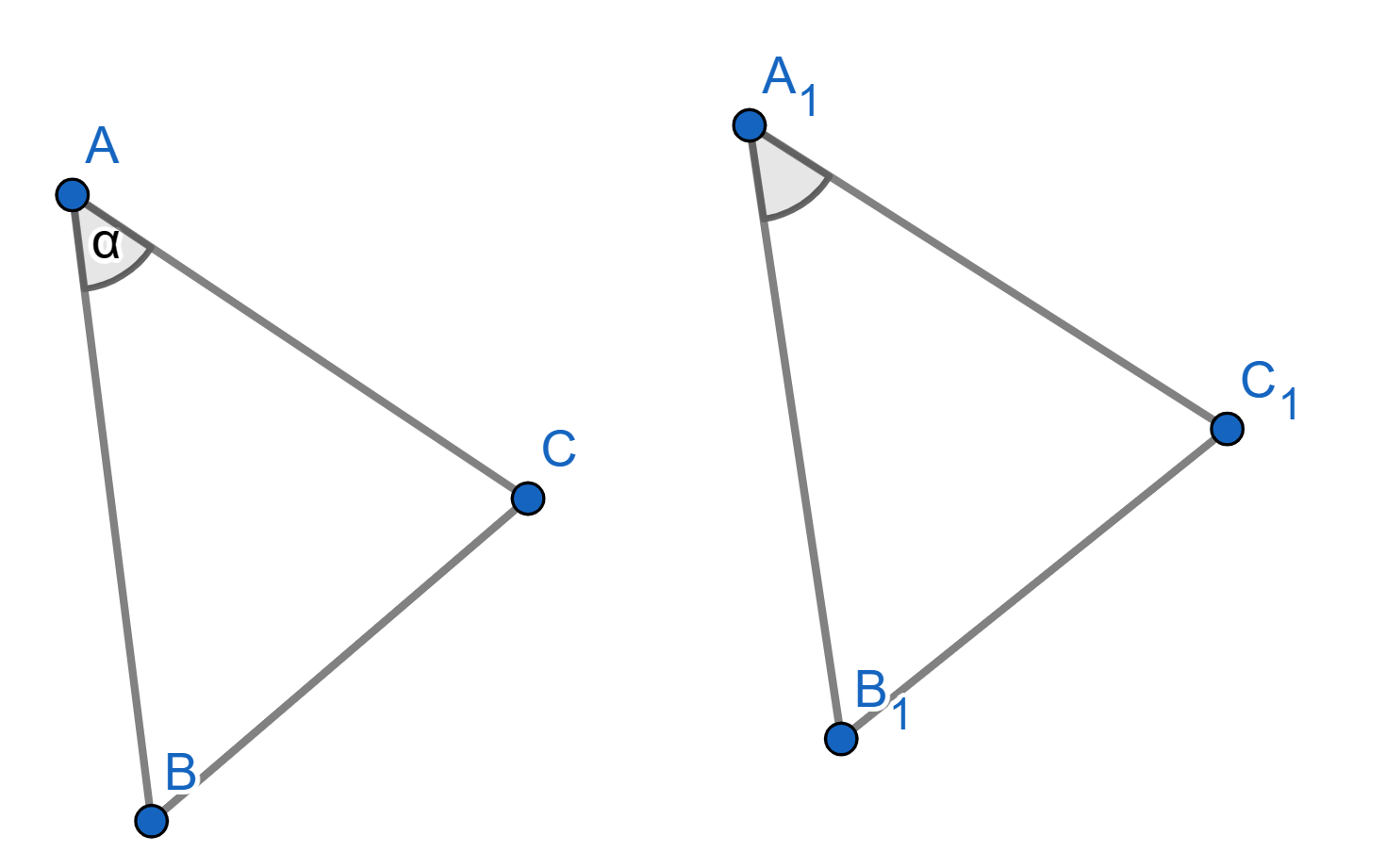
Let \(ABC\) and \(A_1B_1C_1\) be two triangles with the following properties: \(AB = A_1B_1\), \(AC = A_1C_1\), and angles \(\angle BAC = \angle B_1A_1C_1\). Then the triangles \(ABC\) and \(A_1B_1C_1\) are congruent. This is usually known as the “side-angle-side" criterion for congruence.