Problems
Tracey wants each straight line on the plane to only consist of points of two or fewer colours. What is the maximum number of colours she can use to colour the plane?
Georgia decided to only colour grid points - points where lines meet on a sheet of square grid paper. She used red and blue crayons, each at least once. The distance between adjacent grid points is \(1\). Show that there is always a segment of length \(5\) whose ends are different colours.
Banksy used three colours to colour the entire plane: red, green and
gold. Show that there are two points, distance one apart, which are the
same colour.
The same is true if he used \(4\)
colours, including grey for example, but that is significantly more
difficult to show.
This is part of a more general problem of colouring the entire plane with some number of colours and trying to avoid segments of length \(1\) with both ends of the same colour. The question is, how many colours do we need? We know \(7\) is enough and that \(3\) is not enough. The general problem is known as Hadwiger–Nelson problem and was first formulated in 1950, with those bounds found almost immediately. The next piece of progress was only made in 2018, when Aubrey de Grey found a geometrical figure with \(1581\) points (we used only \(7\) in the above proof) that shows it is not possible to only use \(4\) colours. That was later refined to \(510\) points. The general answer of whether it is \(5\), \(6\) or \(7\) colours is still unknown.
Vincent would like to colour the entire \(3\)-dimensional space in such a way that no two points distance \(1\) apart are of the same colour. Prove that he needs at least \(5\) colours.
Let \(\triangle ABC\) and \(\triangle DEF\) be triangles such that the following angles are equal: \(\angle ABC = \angle DEF\) and \(\angle ACB = \angle DFE\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar triangles.
The medians \(AD\) and \(BE\) of the triangle \(\triangle ABC\) intersect at the point \(F\). Prove that \(\triangle AFB\) and \(\triangle DFE\) are similar. What is their similarity coefficient?
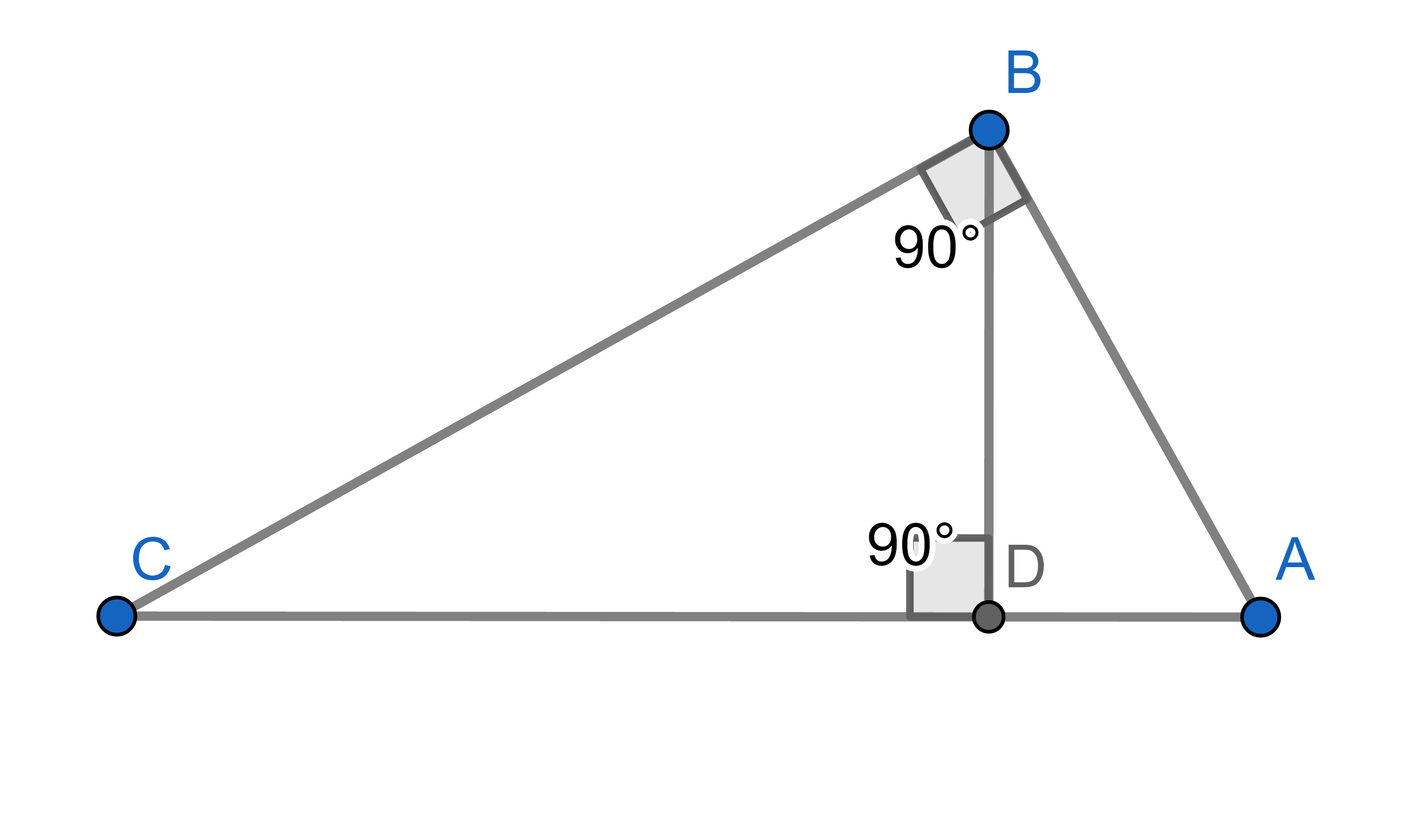
In a triangle \(\triangle ABC\), the angle \(\angle B = 90^{\circ}\) . The altitude from point \(B\) intersects \(AC\) at \(D\). We know the lengths \(|AD|=9\) and \(|CD|=25\). What is the length \(|BD|\)?
Let \(\triangle ABC\) and \(\triangle DEF\) be two triangles such that \(\angle ACB = \angle DFE\) and \(\frac{|DF|}{|AC|} = \frac{|EF|}{|BC|}\). Prove that \(\triangle ABC\) and \(\triangle DEF\) are similar.
Let \(AA_1\) and \(BB_1\) be the medians of the triangle \(\triangle ABC\). Prove that \(\triangle A_1B_1C\) and \(\triangle BAC\) are similar. What is the similarity coefficient?
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\), which intersect at the point \(F\). Prove that \(\triangle AFE\) and \(\triangle BFD\) are similar.