Problems
Let \(AD\) and \(BE\) be the heights of the triangle \(\triangle ABC\). Prove that \(\triangle DEC\) and \(\triangle ABC\) are similar.
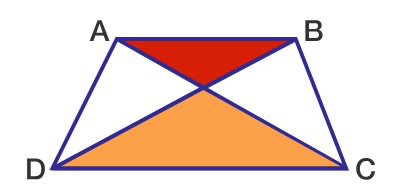
The area of the red triangle is \(25\) and the area of the orange triangle is \(49\). What is the area of the trapezium \(ABCD\)?
Prove that the ratio of perimeters of similar polygons is equal to the similarity coefficient.
Let \(CB\) and \(CD\) be tangents to the circle with the centre \(A\), let \(E\) be the point of intersection of the line \(AC\) with the circle. Draw \(FG\) as the segment of a tangent drawn through the point \(E\) between the lines \(CB\) and \(CD\). Find the length \(|FG|\) if the radius of the circle is \(15\) and \(|AC| = 39\).
Prove that the relation between areas of two similar polygons equals to the square of their similarity coefficient.
In triangle \(\triangle ABC\) with right angle \(\angle ACB=90^{\circ}\), \(CD\) is the height and \(CE\) is the bisector. Draw the bisectors \(DF\) and \(DG\) of the triangles \(BDC\) and \(ADC\). Prove that \(CFEG\) is a square.
Karl and Louie are playing a game. They place action figures around a round table with 24 seats. No two figures are allowed to sit next to each other, regardless of whether they belong to Karl or Louie. The player who cannot place their figure loses the game. Karl goes first - show that Louie can always win.
Katie and Andy play the following game: There are \(18\) chocolate bites on a plate. Each player is allowed to take \(1,2\) or \(3\) bites at once. The person who cannot take any more bites loses. Katie starts. Who has the winning strategy?
Arthur and Dan play the following game. There are \(26\) beads on the necklace. Each boy is allowed to take \(1,2,3\) or \(4\) beads at once. The boy who cannot take any more beads loses. Arthur starts - who will win?
Two goblins, Krok and Grok, are playing a game with a pile of gold. Each goblin takes a positive number of coins, at most \(9\), from the pile. They take turns one after another. There are \(3333\) coins in total and the goblin who takes the last coin wins. Who will win if Krok goes first?