Problems
Oliver throws a fair coin three times. What are his chances of getting three heads, two heads and one tail, one head and two tails, or three tails?
In Pascal’s triangle, what numbers appear in the diagonal next to the positive integers?
Five friends get together and want to take a photo. They all agree that two of them should take a photo of the other three. How many ways can you choose the three people to be in the picture?
In Pascal’s triangle, what’s the sum of the numbers in each row when you put a minus sign in front of every other number?

What is \(11^2\), \(11^3\) and \(11^4\), and what do these numbers have to do with Pascal’s triangle? What goes wrong with \(11^5\)?
How many paths are there from the \(1\) at the top (in the ‘zeroth’ row) to the first \(70\), which appears in the middle of the eighth row?
These paths go down at each step to a number either to the left or to the right. An example is (the first \(1\)), \(1\), \(2\), \(3\), \(6\), \(10\), \(15\), \(35\) and then \(70\) to finish.
What’s the sum of the squares of the numbers in the \(n^{\text{th}}\) row?
Let \(p\) be a prime number. What do you notice about the numbers other than \(1\) in the \(p^{\text{th}}\) row? Can you prove it?
The picture below shows the ‘hockey-stick’ identity in Pascal’s triangle.
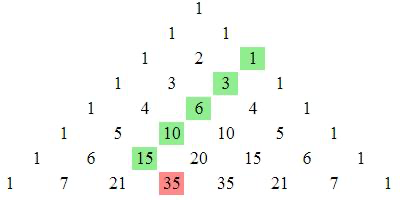
It says that if you start one of the diagonals formed of \(1\)s at the edge, then follow the numbers diagonally in one direction (e.g. left in the picture) and then change direction on your final turn (right in the picture), then the sum of the all but the last number is equal to the last number.
Prove this is true. Written algebraically, \[\binom{r}{r}+\binom{r+1}{r}+...+\binom{n-1}{r}+\binom{n}{r}=\binom{n+1}{r+1},\] where \(0\le r\le n\).
In the \(n^{\text{th}}\) row of Pascal’s triangle, leave the left \(1\) untouched, multiply the next number along (which is \(\binom{n}{1}=n\)) by \(2\), multiply the next number along (which is \(\binom{n}{2}=\frac{n(n-1}{2}\)) by \(4\), and so on, until you multiply the right-hand \(1\) by \(2^n\). That is, multiply the \(k^{\text{th}}\) number from the left by \(2^k\).
Now what’s the sum of the numbers in the \(n^{\text{th}}\) row?