Problems

Bryn calls the date beautiful if all \(6\) digits of the date entry are different. For example: 19.04.23 is a beautiful date, but 19.02.23 and 01.06.23 are not. How many beautiful dates are there in \(2023\)?

On the grid paper, Theresa drew a rectangle \(199 \times 991\) with all sides on the grid lines and vertices on intersection of grid lines. How many cells of the grid paper are crossed by a diagonal of this rectangle?

The school cafeteria offers three varieties of pancakes and five different toppings. How many different pancakes with toppings can Emmanuel order? He has to have exactly one topping on each pancake.

How many six-digit numbers are there whose digits all have the same parity? That is, either all six digits are even, or all six digits are odd.

Donald’s sister Maggie goes to a nursery. One day the teacher at the nursery asked Maggie and the other children to stand a circle. When Maggie came home she told Donald that it was very funny that in the circle every child held hands with either two girls or two boys. Given that there were five boys standing in the circle, how many girls were standing in the circle?

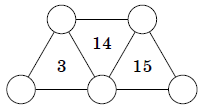
Michael used different numbers \(\{0,1,2,3,4,5,6,7,8,9\}\) to put in the circles in the picture below, without using any one of them twice. Inside each triangle he wrote down either the sum or the product of the numbers at its vertices. Then he erased the numbers in the circles. Which numbers need to be written in circles so that the condition is satisfied?

Solve the puzzle: \[\textrm{AC}\times\textrm{CC}\times\textrm{K} = 2002.\] Different letters correspond to different digits, identical letters correspond to identical digits.

• We call two figures congruent if their corresponding sides and angles are equal. Let \(ABD\) an \(A'B'D'\) be two right-angled triangles with right angle \(D\). Then if \(AD=A'D'\) and \(AB=A'B'\) then the triangles \(ABD\) and \(A'B'D'\) are congruent.

• It follows from the previous statement that if two lines \(AB\) and \(CD\) are parallel than angles \(BCD\) and \(CBA\) are equal.

We prove the other two assertions from the description:

• The sum of all internal angles of a triangle is also \(180^{\circ}\).

• In an isosceles triangle (which has two sides of equal lengths), two angles touching the third side are equal.

In the triangle \(ABC\) the sides are compared as following: \(AC>BC>AB\). Prove that the angles are compared as follows: \(\angle B > \angle A > \angle C\).