Problems

It is known that \(a + b + c = 5\) and \(ab + bc + ac = 5\). What are the possible values of \(a^2 + b^2 + c^2\)?

Prove the magic trick for the number \(1089 = 33^2\): if you take any \(3\)-digit number \(\overline{abc}\) with digits coming in strictly descending order and subtract from it the number obtained by reversing the digits of the original number \(\overline{abc} - \overline{cba}\) you get another \(3\)-digit number, call it \(\overline{xyz}\). Then, no matter which number you started with, the sum \(\overline{xyz} + \overline{zyx} = 1089\).
Recall that a number \(\overline{abc}\) is divisible by \(11\) if and only if \(a-b+c\) also is.

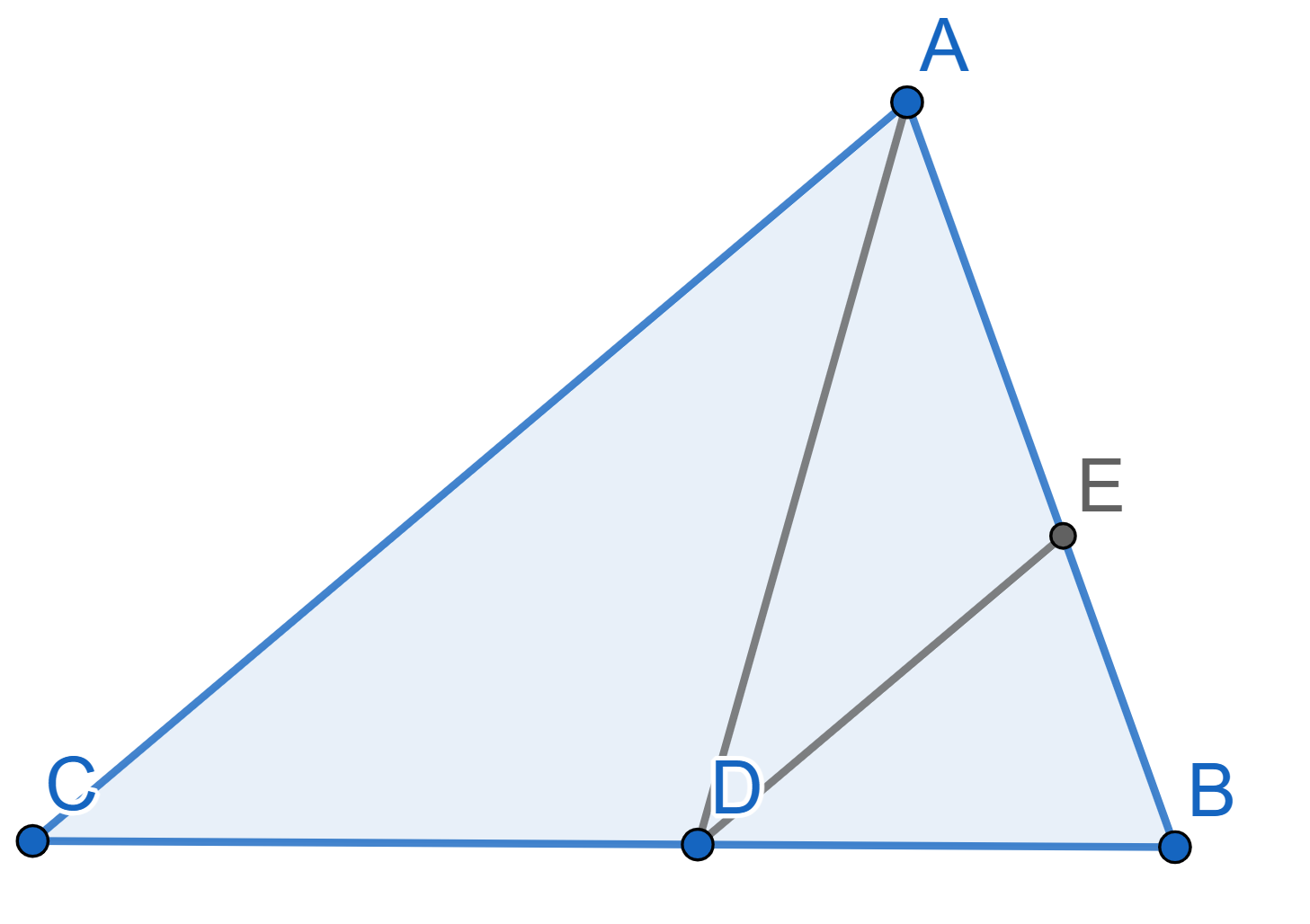
On the diagram below \(AD\) is the bisector of the triangle \(ABC\). The point \(E\) lies on the side \(AB\), with \(AE = ED\). Prove that the lines \(AC\) and \(DE\) are parallel.

Do there exist two numbers such that their sum, quotient and product would be all equal to each other?

It is easy to construct one equilateral triangle using three identical matches. Is it possible to construct four equilateral triangles by adding just three more matches identical to the original ones?

Winnie the Pooh has five friends, each of whom has pots of honey in their house: Tigger has \(1\) pot, Piglet has \(2\), Owl has \(3\), Eeyore has \(4\), and Rabbit has \(5\). Winnie the Pooh comes to visit each friend in turn, eats one pot of honey and takes the other pots with him. He came into the last house carrying \(10\) pots of honey. Whose house could Pooh have visited last?

Find the largest possible number of bishops that can be placed on the \(8 \times 8\) chessboard so that no two bishops threaten each other.

Does there exist a power of \(3\) that ends in \(0001\)?

There are \(24\) children in a class. Some pairs of children are friends. The friendship relation satisfies the following rules:

• If someone (say Alice) is a friend of someone else (say Bob), then Bob is a friend of Alice.

• If Alice is a friend of Bob and Bob is a friend of Claire, then Alice is also a friend of Claire.

Therefore Alice must be friends with herself. Is this reasoning correct?

I am going to convince you that all people have the same eye color! How? Well, notice that if there were only one person in the world, then my claim would be true. Now we will explain that if the claim is true when there are \(n\) people in the world, then it will also be true when there are \(n+1\) people. Therefore, it will be true regardless of the amount of people! (This kind of proof is called a proof by induction)

Let’s imagine that the claim is true when there are \(n\) people in the world. Now take any group of \(n+1\) people, and label them \(a_1,a_2,\dots,a_{n+1}\). Remove \(a_1\). The remaining people \(a_2,a_3,\cdots,a_{n+1}\) form a group of \(n\) people, so they must all have the same eye colour.

On the other hand, let’s remove \(a_{n+1}\). The remaining people \(a_1,a_2,\dots,a_{n}\) also form a group of \(n\) people, so they must again all have the same eye colour.

Since these two smaller groups overlap (they both contain \(a_2,a_3,\dots,a_{n-1}\)), everyone in the full group \(a_1,a_2,\dots,a_n\) has the same eye colour.