Problems

We are going to show that \(1\) is the largest natural number.
Proof: Let \(n\) be the largest natural number. We will show that \(n=1\). Since \(n\) is the largest natural number, \(n^2\), which is also a natural number, must be less than or equal to \(n\). Therefore \(n^2-n\leq 0\). But \(n^2-n=n(n-1)\). If \(n(n-1)\leq 0\), it must be that \(0\leq n\leq 1\), and so \(n=1\).

Recall that \((n+1)^2=n^2+2n+1\). Subtracting \(2n+1\) from both sides gives \((n+1)^2-(2n+1)=n^2\). Now subtract \(n(2n+1)\) from both sides to obtain \((n+1)^2-(2n+1)-n(2n+1)=n^2-n(2n+1)\). Notice that the left-hand side can be rewritten as \((n+1)^2-(n+1)(2n+1)\), so we have \((n+1)^2-(n+1)(2n+1)=n^2-n(2n+1)\).

Next, add \(\frac{(2n+1)^2}{4}\) to both sides. This allows us to complete the square on each side, giving \(((n+1)-\frac{2n+1}{2})^2=(n-\frac{2n+1}{2})^2\).

Taking square roots of both sides leads to \((n+1)-\frac{2n+1}{2}=n-\frac{2n+1}{2}\). Adding \(\frac{2n+1}{2}\) to both sides produces \(n+1=n\), which simplifies to \(1=0\).

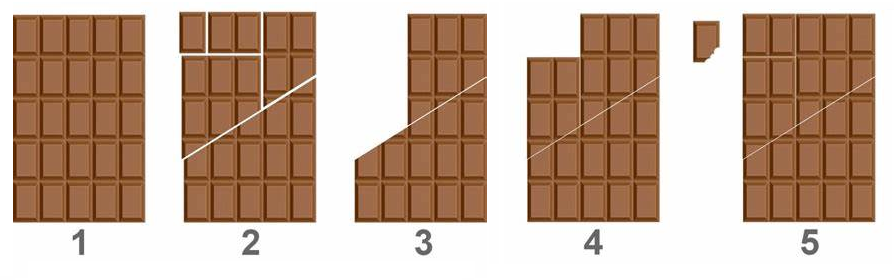
This problem is often called "The infinite chocolate bar". Depicted below is a way to get one more piece of chocolate from the \(5\times 6\) chocolate bar. Do you see where is it wrong?

Let’s prove that \(1=2\). Take a number \(a\) and suppose \(b=a\). After multiplying both sides we have \(a^2=ab\). Subtract \(b^2\) from both sides to get \(a^2-b^2=ab-b^2\). The left hand side is a difference of two squares so \((a-b)(a+b)=b(a-b)\). We can cancel out \(a-b\) and obtain that \(a+b=b\). But remember from the start that \(a=b\), so substituting \(a\) for \(b\) we see that \(2b=b\), dividing by \(b\) we see that \(2=1\).

In how many ways can you read the word TRAIN from the picture below, starting from T and going either down or right at each step?

John drunk a \(\frac16\) of a full cup of black coffee and then filled the cup back up with milk. Then he drunk a third of what he had in the cup. Then, he refilled it back to full with milk again, and after that, drunk a half of the cup. Finally, he once again refilled the cup with milk and drunk everything he had. What did he drink more of - coffee or milk?

A round necklace contains \(45\) beads of two different colours: red and blue. Show that it is possible to find two beads of the same colour next to each other.

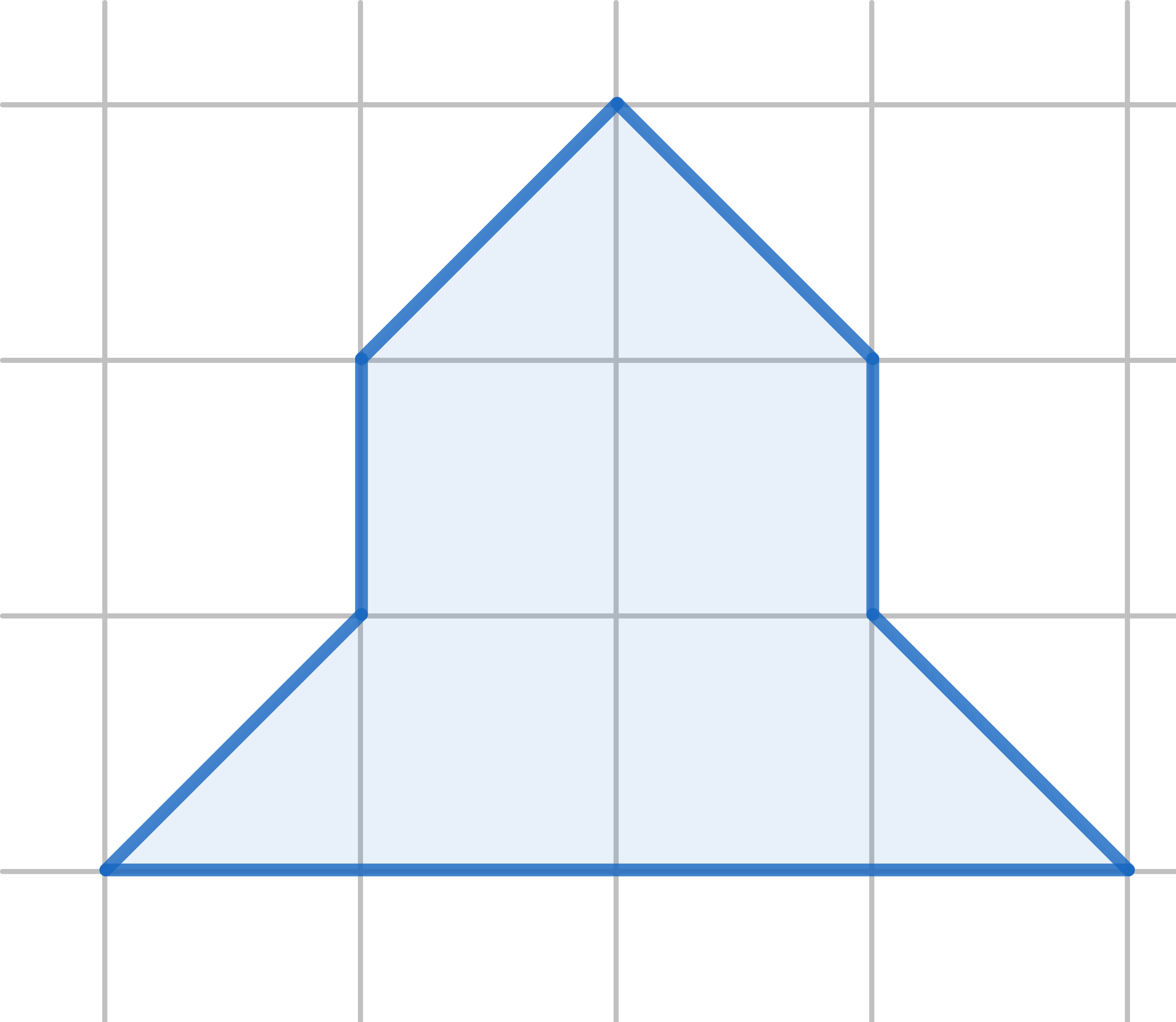
Cut this figure into \(4\) identical shapes. (Note: you have to use the entire shape. Rotations and reflections count as identical shapes)

Find the last two digits of the number \[33333333333333333347^4 - 11111111111111111147^4\]

Replace all stars with ”+” or ”\(\times\)” signs so the equation holds: \[1*2*3*4*5*6=100\] Extra brackets may be added if necessary. Please write down the expression into the answer box.