Problems

There are \(15\) lightbulbs in a row, all switched off. We can pick any three of them and change their state. Can we repeat this operation an even number of times such that at the end all the lightbulbs are on?

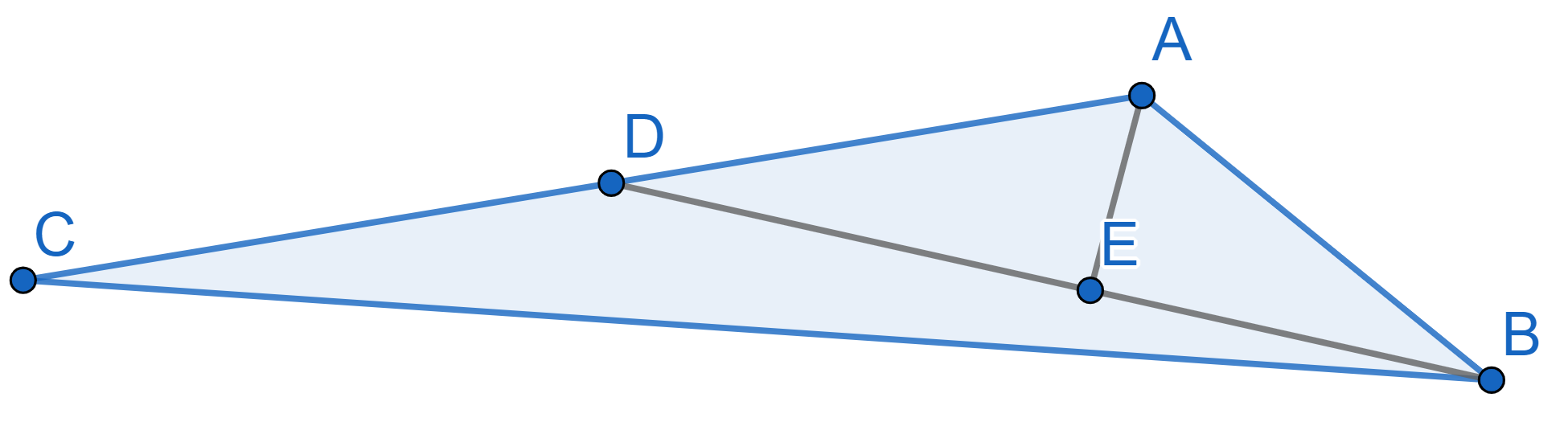
In the triangle \(ABC\) the segment \(AB=5\) and the segment \(BD\) is the median. The segment \(AE\) is perpendicular to \(BD\) and divides \(BD\) in half. Find the length of \(AC\).

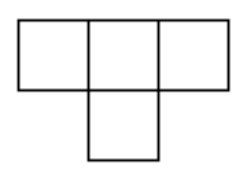
Can you cover a \(10 \times 10\) board using only \(T\)-shaped tetrominos?

Can you cover a \(10 \times 10\) square with \(1 \times 4\) rectangles?

Two opposite corners were removed from an \(8 \times 8\) chessboard. Is it possible to cover this chessboard with \(1 \times 2\) rectangular blocks?

One unit square of a \(10 \times 10\) square board was removed. Is it possible to cover the rest of it with \(3\)-square \(L\)-shaped blocks?

Is it possible to cover a \(10 \times 10\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.

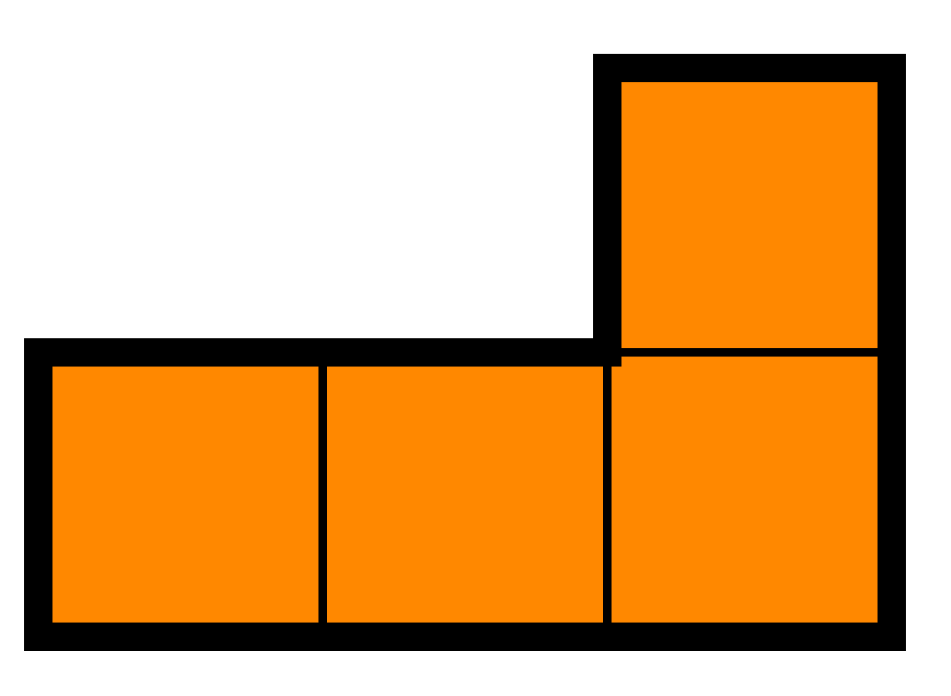
In an \(5\times 5\) board one corner was removed. Is it possible to cover the remaining board with linear trominos (\(1\times 3\) blocks)?

Convert the binary number \(10011\) into decimal, and convert the decimal number \(28\) into binary. Multiply by \(2\) as binary numbers both \(10011\) and the result of conversion of \(28\) into binary numbers.

The ternary numeral system has only \(3\) digits: \(0,\) \(1\) and \(2\). Therefore the number \(3\) is written in ternary as \(10\). Write down the numbers \(23\) and \(156\) in ternary and add them as ternary.