Problems

Write down the first fifteen numbers in binary system.

Roman numerals are a numeral system that originated in ancient Rome and remained the usual way of writing numbers throughout Europe well into the Late Middle Ages. Numbers are written as combinations of letters from the Latin alphabet, each letter with a fixed integer value:

I&V&X&L&C&D&M
1&5&10&50&100&500&1000

For example the first \(12\) numbers in Roman Numerals are written as: \(I,\,II,\, III,\, IV,\, V,\, VI,\, VII,\, VIII,\, IX,\, X,\, XI,\, XII\), where the notations \(IV\) and \(IX\) can be read as "one less than five" and "one less than ten" correspondingly. A number containing two or more decimal digits is built by appending the Roman numeral equivalent for each digit, from highest to lowest, as in the following examples: the current year \(2024\) as \(MMXXIV\), number \(17\) as \(XVII\) and number \(42\) as \(XLII\) or \(XXXXII\). Let’s see how to multiply Roman numerals by multiplying \(17\) and \(42\).

Write down in Roman numerals the numbers \(14\) and \(61\) and multiply them as Roman numerals.

Two lines \(CD\) and \(CB\) are tangent to a circle with the center \(A\) and radius \(R\), see the picture. The angle \(\angle BCD\) equals \(120^{\circ}\). Find the length of \(BD\) in terms of \(R\).

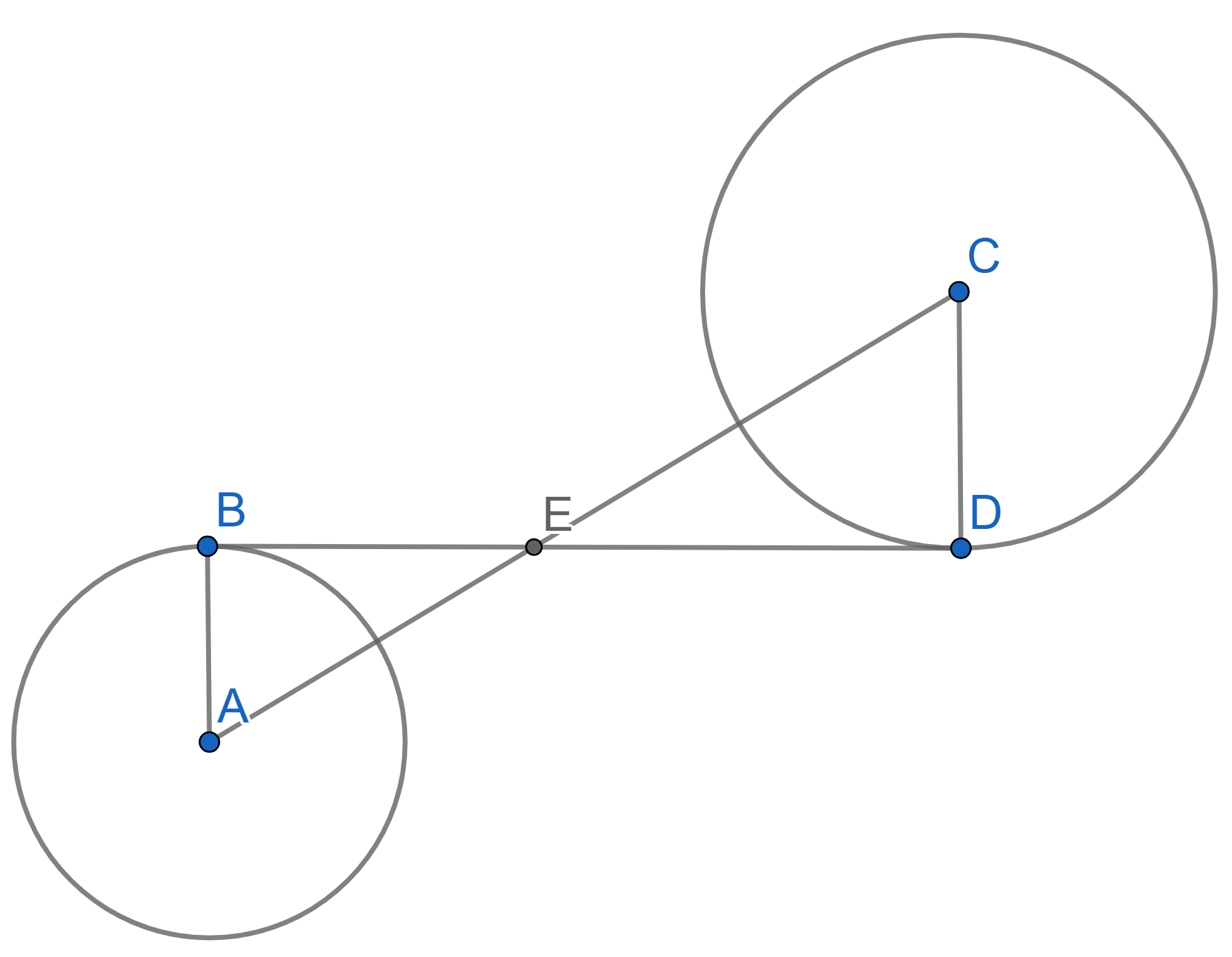
Given two circles, one has centre \(A\) and radius \(r\), another has centre \(C\) and radius \(R\). Both circles are tangent to a line at the points \(B\) and \(D\) respectively and the angles \(\angle CED = \angle AEB = 30^{\circ}\). Find the length of \(AC\) in terms of \(r\) and \(R\).

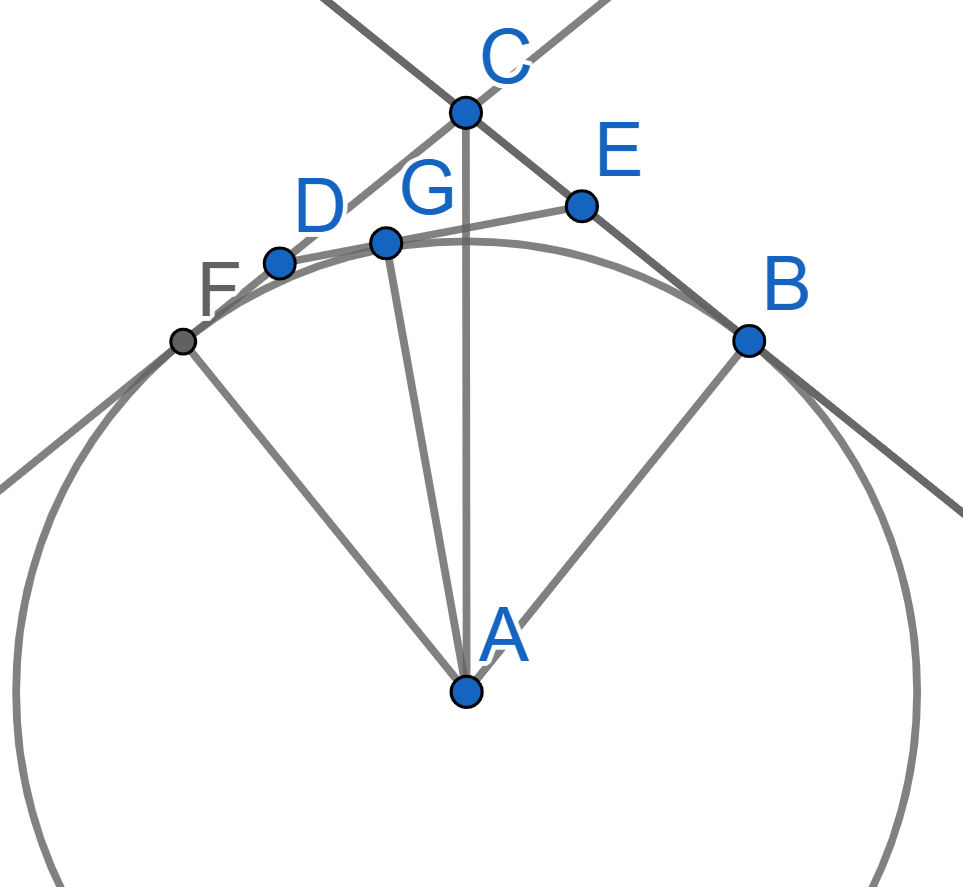
Consider a triangle \(CDE\). The lines \(CD\), \(DE\), and \(CE\) are tangent to a circle with centre \(A\) at the points \(F,G\), and \(B\) respectively. We also have that the angle \(\angle DCE = 120^{\circ}\). Prove that the length of the segment \(AC\) equals the perimeter of the triangle \(CDE\).

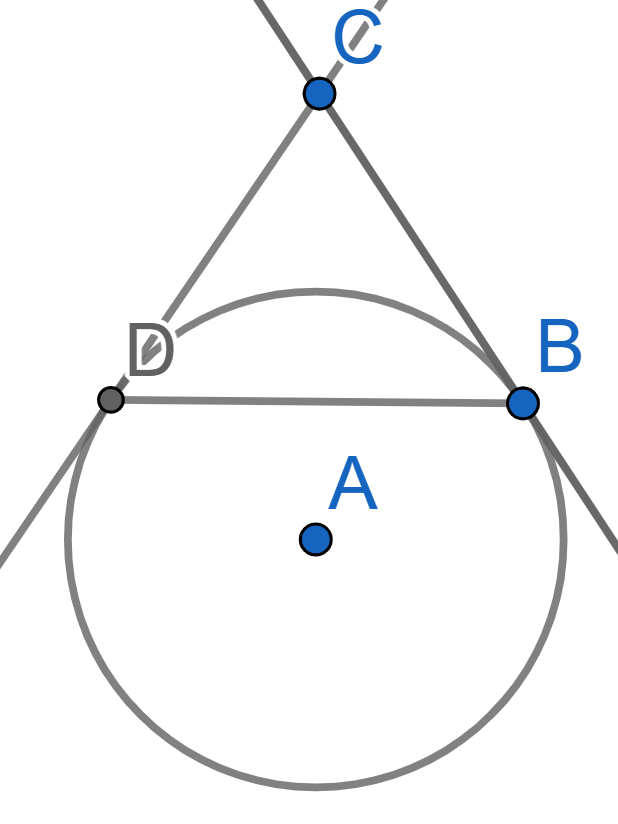
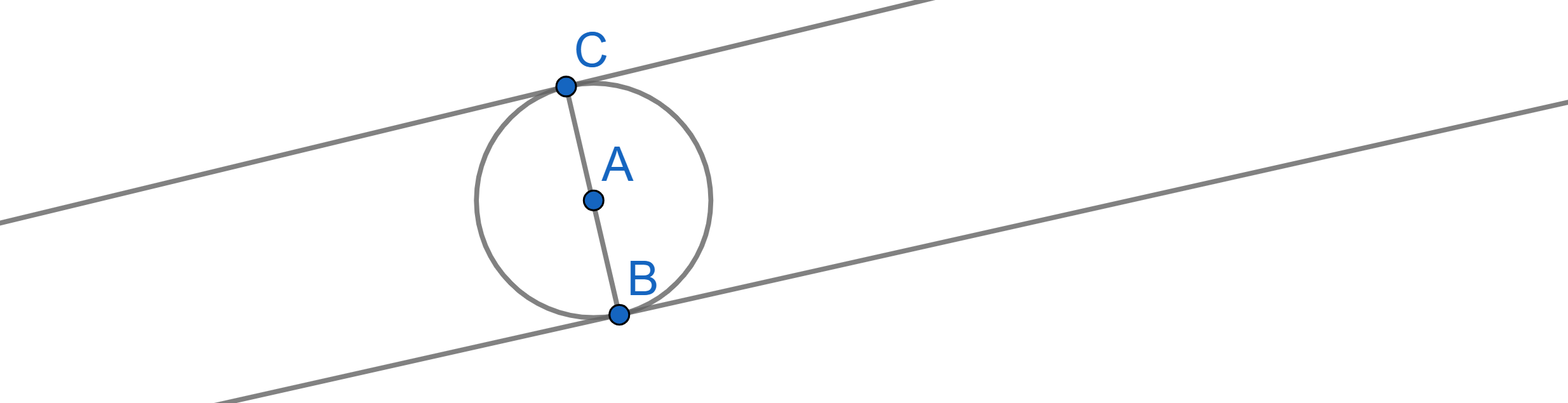
A circle with center \(A\) is tangent to the lines \(CB\) and \(CD\), see picture. Find the angles of the triangle \(BCD\) if \(BD=BC\).

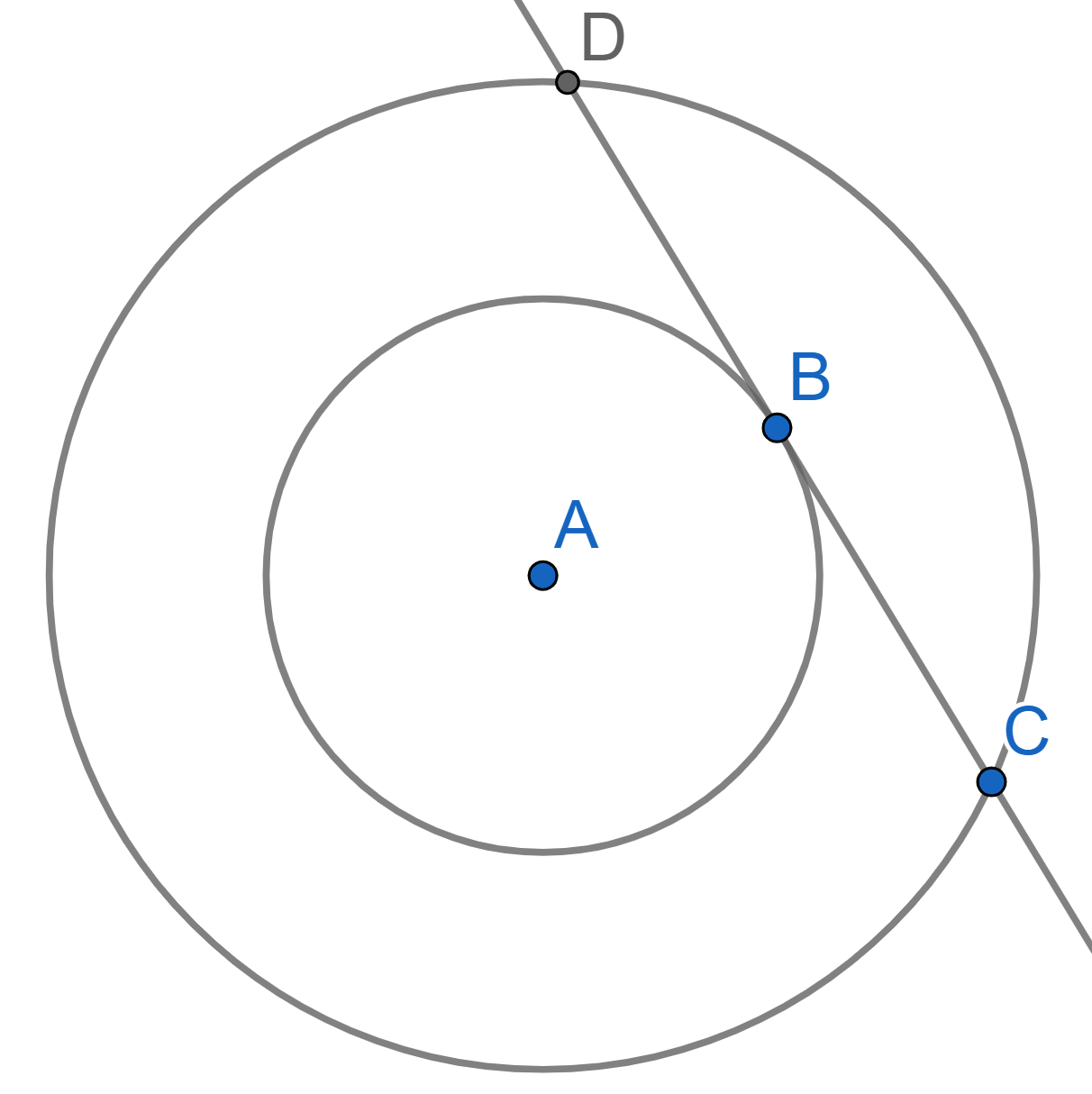
Take two circles with a common centre \(A\). A chord \(CD\) of the bigger circle is tangent to the smaller one at the point \(B\). Prove that \(B\) is the midpoint of \(CD\).

Prove that the lines tangent to a circle in two opposite points of a diameter are parallel.

Show for positive \(a\) and \(b\) that \(a^2 +b^2 \ge 2ab\).