Problems

Is it true that if \(b\) is a positive number, then \(b^3 + b^2 \ge b\)? What about \(b^3 +1 \ge b\)?

Show that if \(a\) is positive, then \(1+a \ge 2 \sqrt{a}\).

Let \(k\) be a natural number, prove the following inequality. \[\frac1{k^2} > \frac1{k} - \frac1{k+1}.\]

Show that if \(a\) is a positive number, then \(a^3+2 \ge 2a \sqrt{a}\).

Consider the following sum: \[\frac1{1 \times 2} + \frac1{2 \times 3} + \frac1{3 \times 4} + \dots\] Show that no matter how many terms it has, the sum will never be larger than \(1\).

Is it possible to cover a \(6 \times 6\) board with the \(L\)-tetraminos without overlapping? The pieces can be flipped and turned.

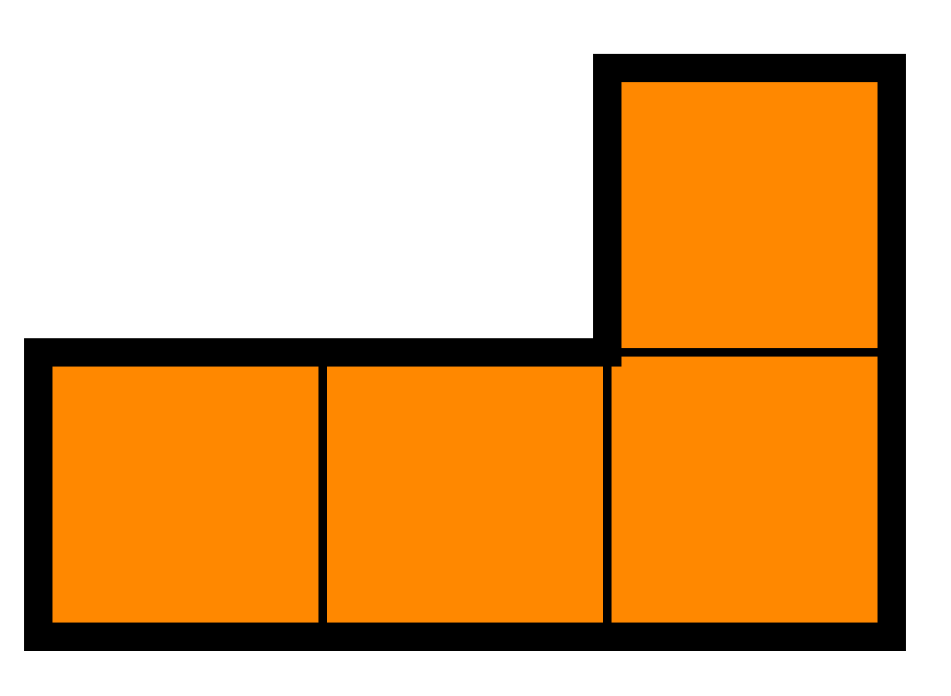
Is it possible to cover a \(4n \times 4n\) board with the \(L\)-tetraminos without overlapping for any \(n\)? The pieces can be flipped and turned.

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a square.

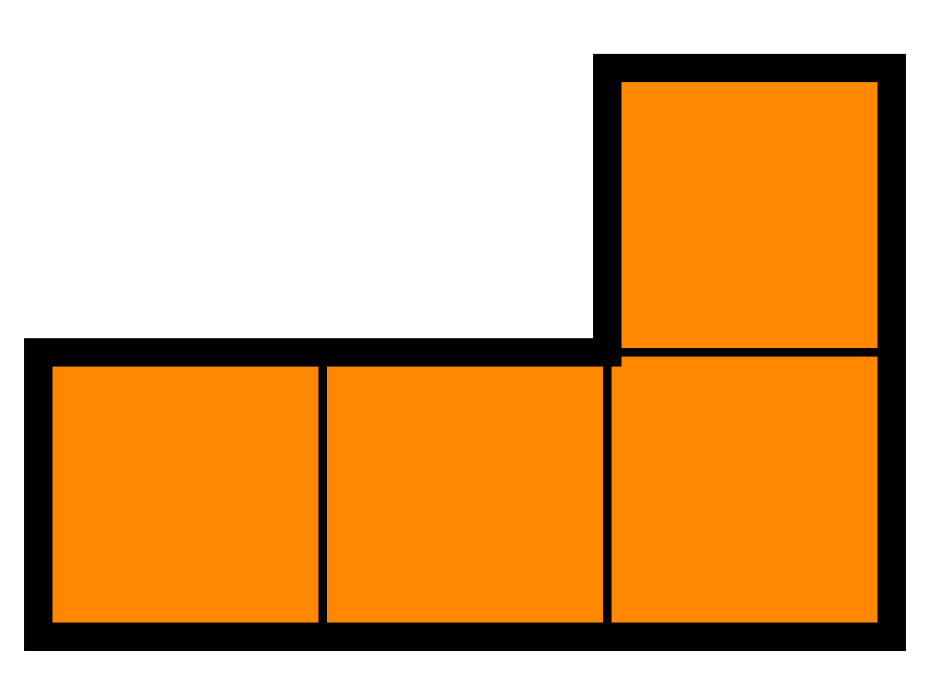
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in an area of the following shape:

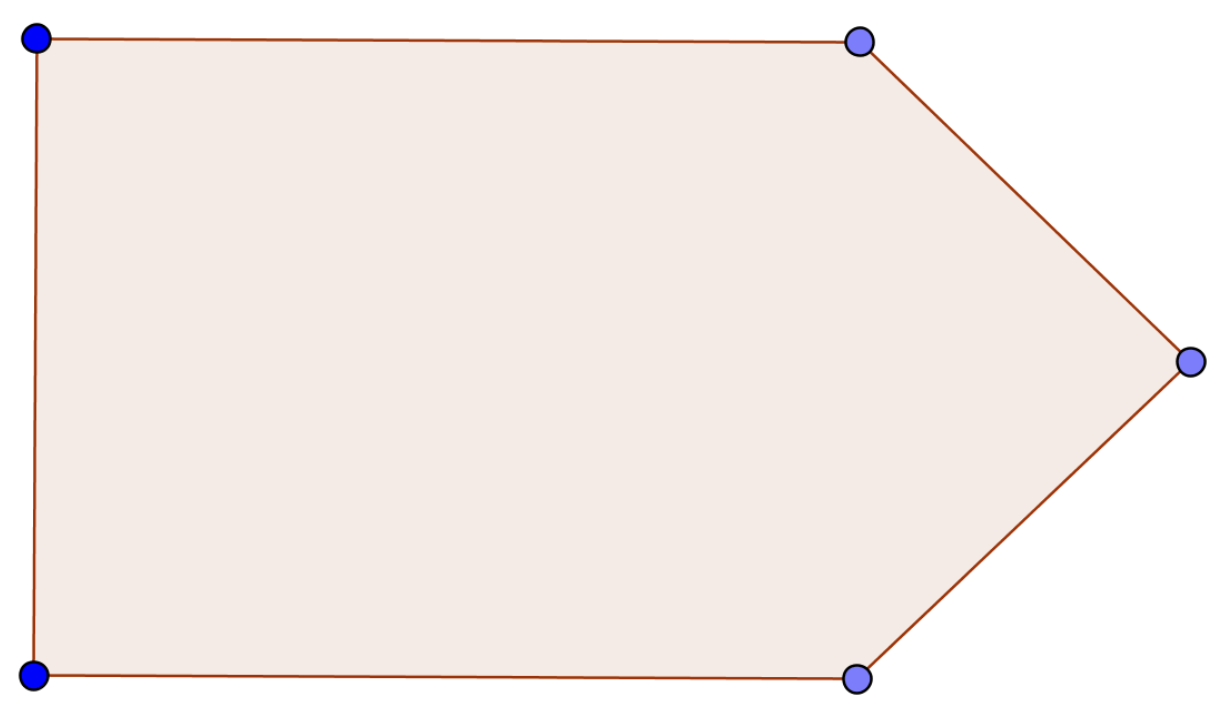
Draw how Robinson Crusoe should put pegs and ropes to tie his goat in order for the goat to graze grass in the shape of a given triangle.