Problems

Is it possible to split \(44\) balls into \(9\) piles so that the number of balls in different piles is different? (Each pile has to have at least one ball)

An ice cream machine distributes ice cream randomly. There are 5 flavours in the machine and you would like to have one of the available flavours at least 3 times, although you don’t mind which flavour it is. How many samples do you need to obtain in total to ensure that?

Determine all prime numbers \(p\) such that \(5p+1\) is also prime.

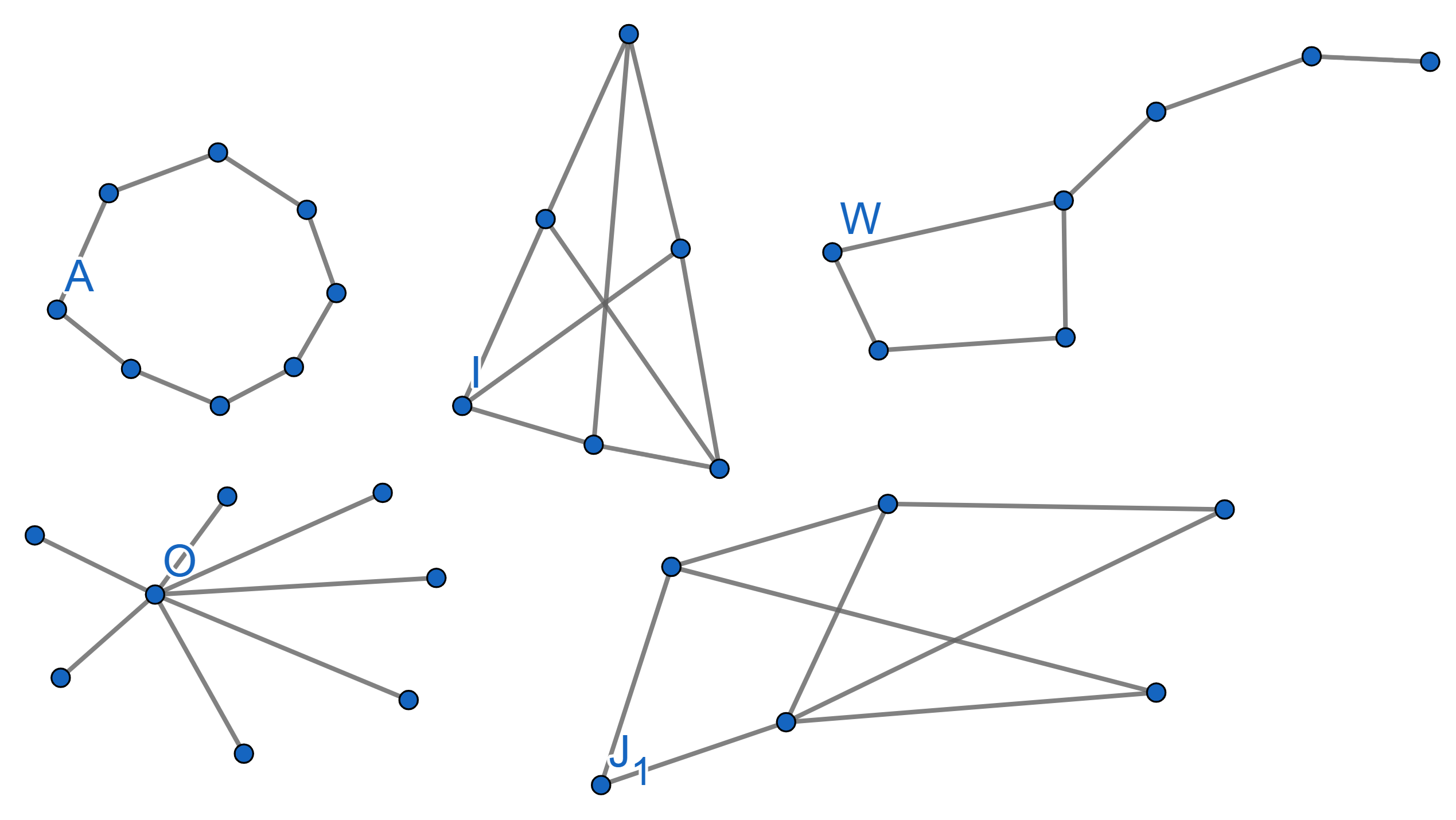
A graph is called Bipartite if it is possible to split all its vertices into two groups in such a way that there are no edges connecting vertices from the same group. Find out whic of the following graphs are bipartite and which are not:

The next day you have even harder situation: to the hotel, where all the rooms are occupied arrives a bus with infinitely many new customers. In the bus all the seats have numbers \(1,2,3...\) corresponding to all natural numbers. How to deal with this one?

What would you do about \(10000\) new guests arriving to the full hotel?

Imagine you have now a general finite number of new guests arriving to the full hotel. What do you do?

On a \(10\times 10\) board, a bacterium sits in one of the cells. In one move, the bacterium shifts to a cell adjacent to the side (i.e. not diagonal) and divides into two bacteria (both remain in the same new cell). Then, again, one of the bacteria sitting on the board shifts to a new adjacent cell, either horizontally or vertically, and divides into two, and so on. Is it possible for there to be an equal number of bacteria in all cells after several such moves?

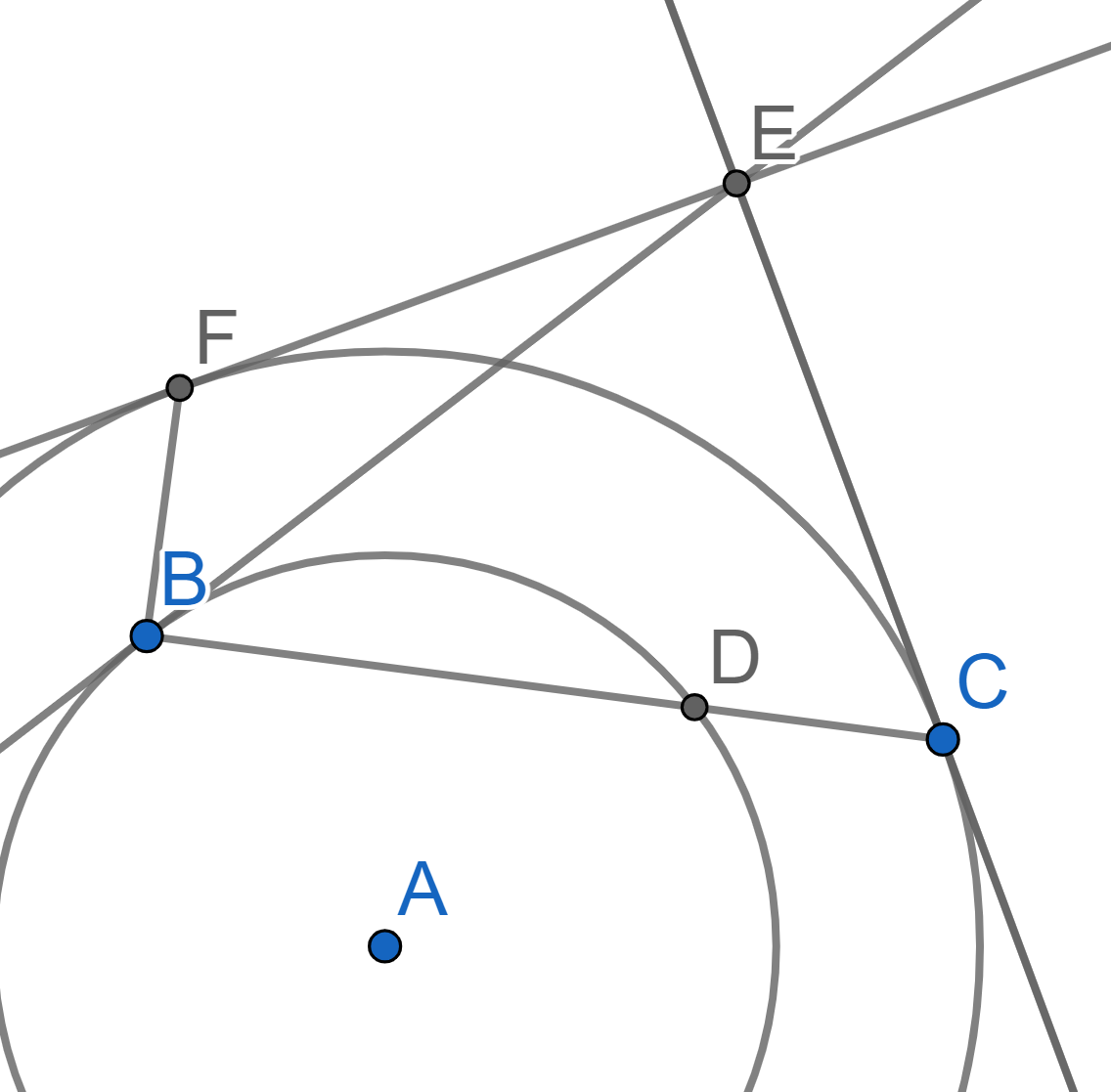
Let \(C_1\) and \(C_2\) be two concentric circles with \(C_1\) inside \(C_2\) and the center \(A\). Let \(B\) and \(D\) be two points on \(C_1\) that are not diametrically opposite. Extend the segment \(BD\) past \(D\) until it meets the circle \(C_2\) in \(C\). The tangent to \(C_2\) at \(C\) and the tangent to \(C_1\) at \(B\) meet in a point \(E\). Draw from \(E\) the second tangent to \(C_2\) which meets \(C_2\) at the point \(F\). Show that \(BE\) bisects angle \(\angle FBC\).

Due to a mistake in the bakery, a cake that was supposed to be shaped as two concentric pieces (like on the right diagram below) came out like the left diagram below. Find the smallest number of pieces the cake should be cut into in order to rearrange the pieces into the cake on the right side of the picture.

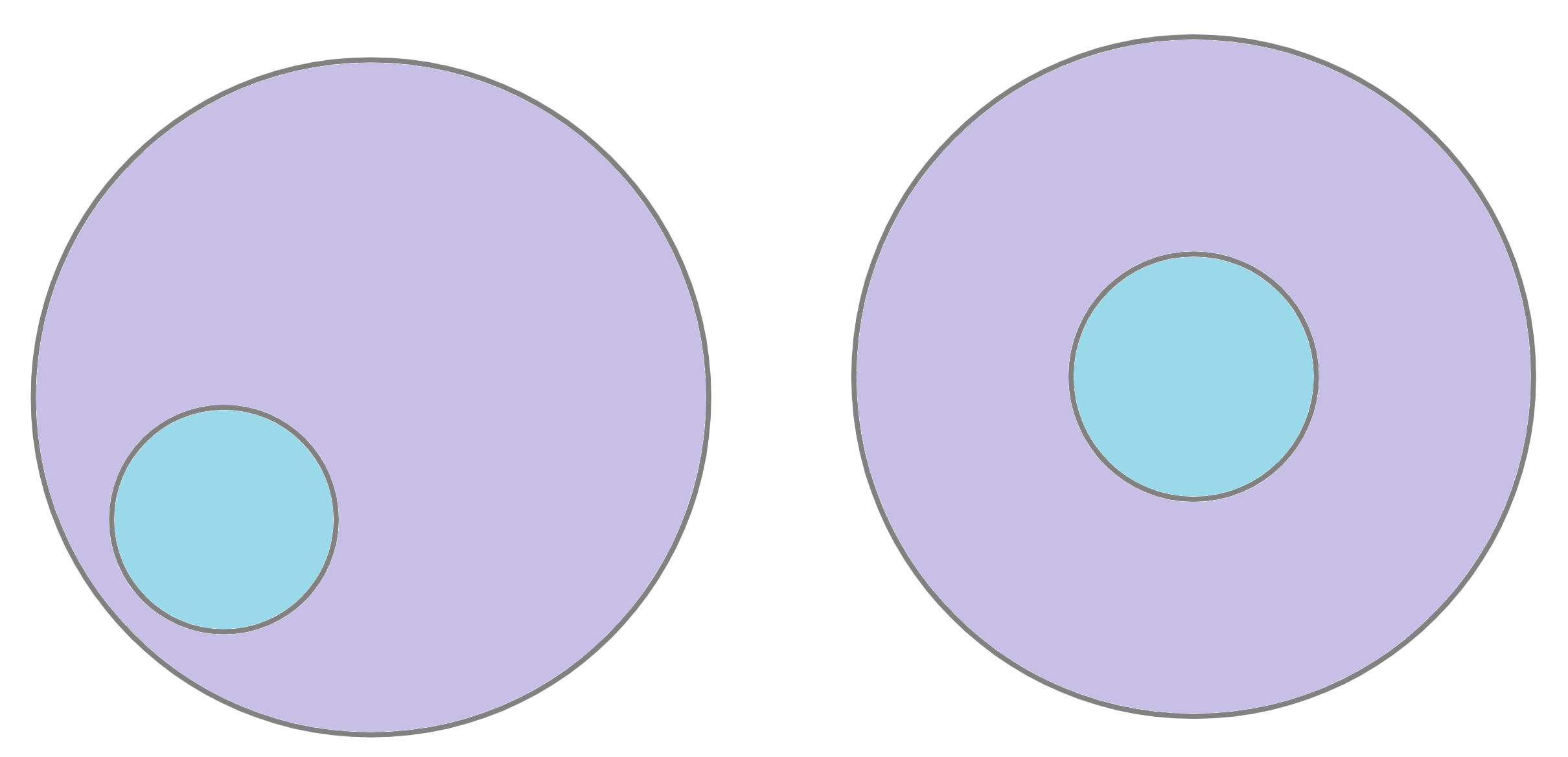
Note that the cake is \(\textit{not}\) tiered like a wedding cake, but is shaped like a cylinder with a flat top. Curved cuts are allowed.