Problems
Can you come up with a divisibility rule for \(5^n\), where \(n=1\), \(2\), \(3\), . . .? Prove that the rule works.
Show that for each \(n=1\), \(2\), \(3\), . . ., we have \(n<2^n\).
You and I are going to play a game. We have one million grains of sand in a bag. We take it in turns to remove \(2\), \(3\) or \(5\) grains of sand from the bag. The first person that cannot make a move loses.
Would you go first?
For every natural number \(k\ge2\), find two combinations of \(k\) real numbers such that their sum is twice their product.
Show that \(n^2+n+1\) is not divisible by \(5\) for any natural number \(n\).
Prove the following identity for any three non-zero real numbers \(a,b,c\): \[\frac{b}{2a} + \frac{c^2 + ab}{4bc} - \left|{\frac{c^2 - ab}{4bc}} \right| - \left|{\frac{b}{2a} - \frac{c^2 + ab}{4bc} + \left|{\frac{c^2 - ab}{4bc}}\right|}\right| = \min\{\frac{b}{a},\frac{c}{b},\frac{a}{c}\}.\]
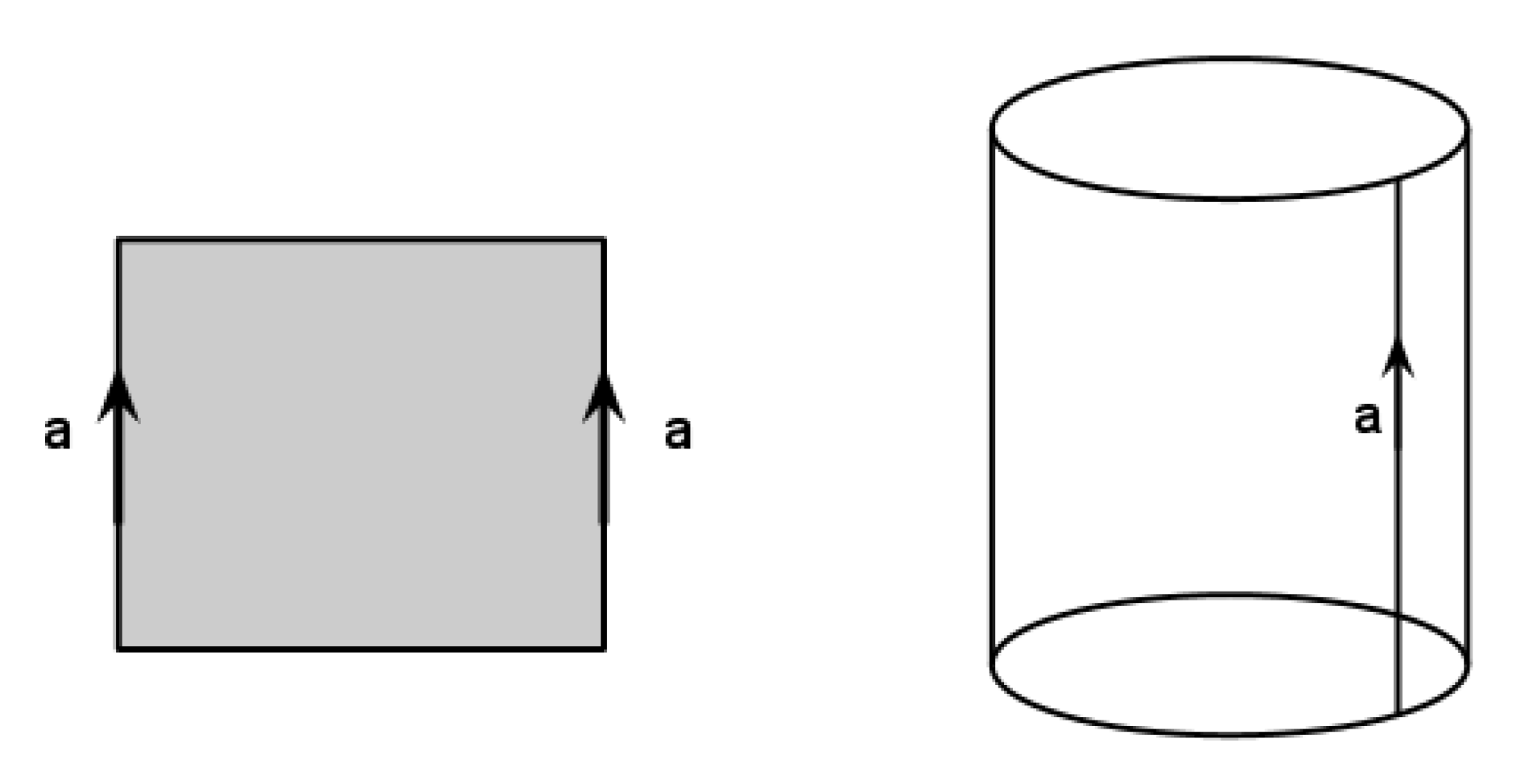
If we glue the opposite sides of the paper band in the same direction as on the picture, we will get a cylinder. What surface do we get, if we glue the circles of the cylinder in the same direction as well?
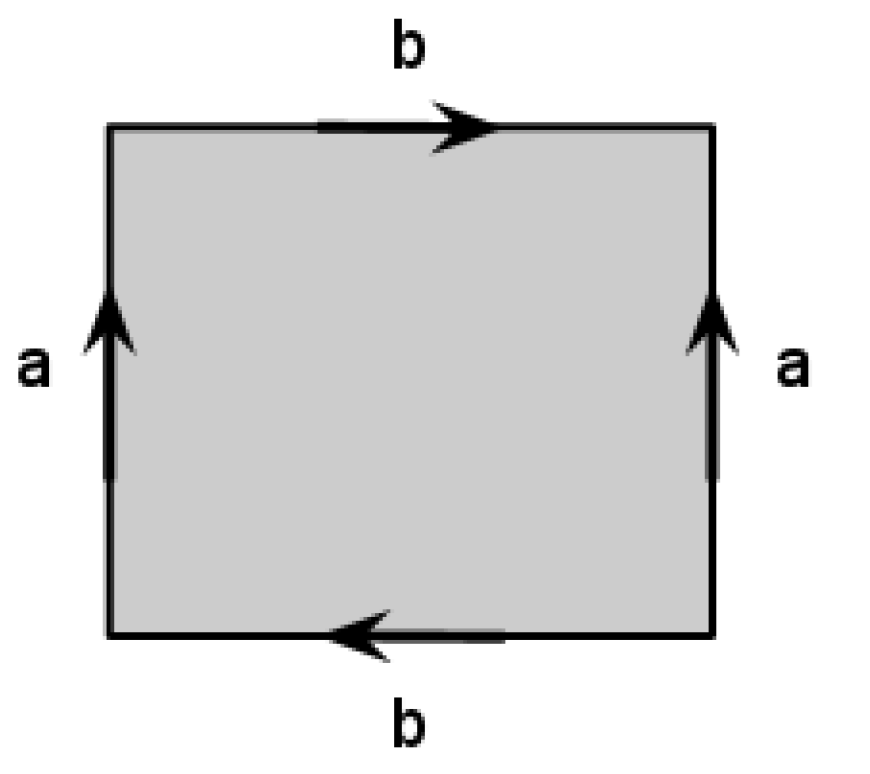
We start with a rectangular sheet of paper - preferably with proportions more than \(6:1\), so that it looks more like a band. For now assume that one can stretch or shrink the paper band as needed. Describe the surface we get if we start with a rectangular sheet of paper and then glue the opposite sides of the paper band in the opposite direction as in the picture.
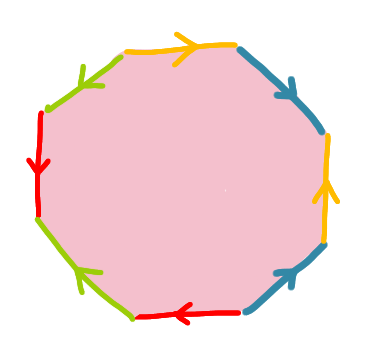
How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.
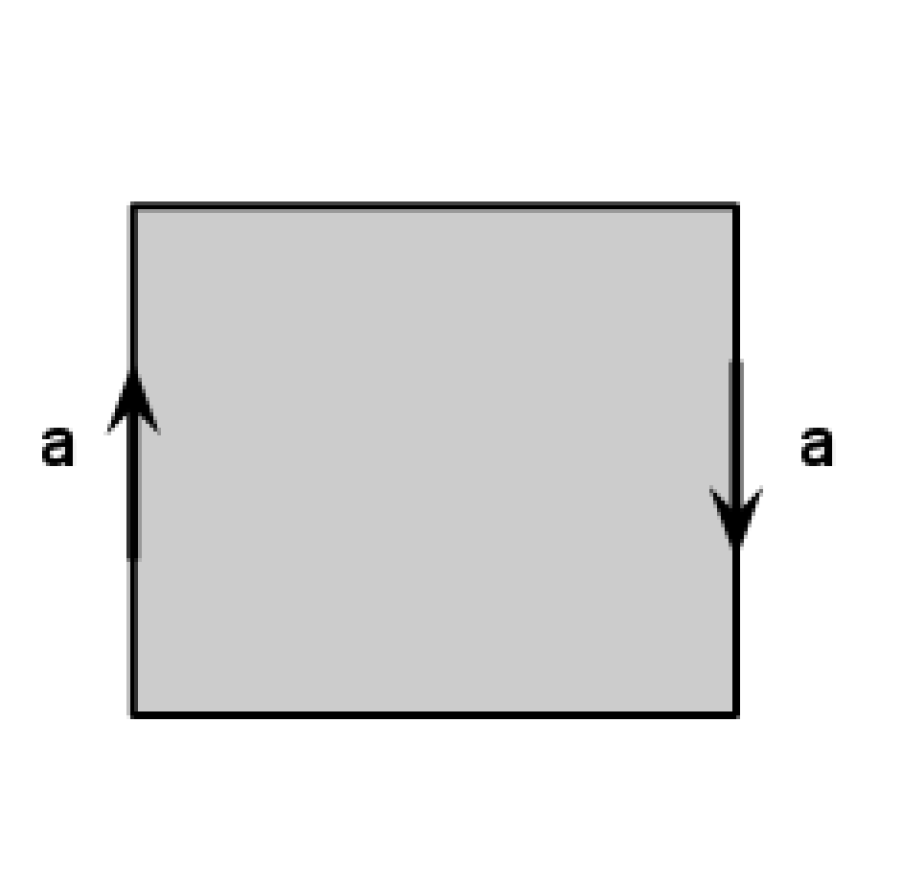
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.