Problems

How would you describe the surface obtained by glueing the sides of the octagon as on the picture? Sides of the same colour are glued together in the same direction as shown.

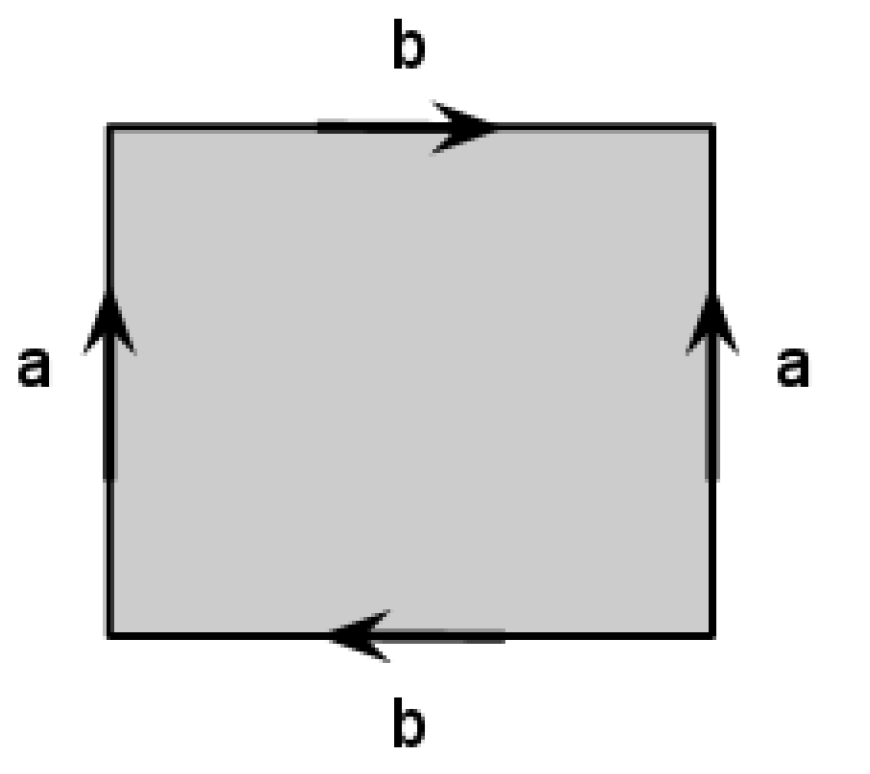
Describe the surface which we can get if we start with a rectangular sheet of paper, make a cylinder by glueing the opposite sides in the same direction and then glue the other opposite sides of the paper band in the opposite direction as on the picture.

A parliament has 650 members. In this parliament there is only one house and every member has at most three enemies. We wish to split this parliament into two separate houses in such a way that each member will have at most one enemy in the same house as them. We assume that hard feelings among members of parliament are mutual, namely if \(A\) recognises \(B\) as their enemy, then \(B\) also recognises \(A\) as their enemy.

Is this splitting possible?

Prove that \(|x|\ge x\). It may be helpful to compare each of \(|3|\), \(|-4.3|\) and \(|0|\) with \(3\), \(-4.3\) and \(0\) respectively.

Let \(A=\{1,2,3\}\) and \(B=\{2,4\}\) be two sets containing natural numbers. Find the sets: \(A\cup B\), \(A\cap B\), \(A-B\), \(B-A\).

Let \(A=\{1,2,3,4,5\}\) and \(B=\{2,4,5,7\}\) be two sets containing natural numbers. Find the sets: \(A\cup B\), \(A\cap B\), \(A-B\), \(B-A\).

Given three sets \(A,B,C\). Prove that if we take a union \(A\cup B\) and intersect it with the set \(C\), we will get the same set as if we took a union of \(A\cap C\) and \(B\cap C\). Essentially, prove that \((A\cup B)\cap C = (A\cap C)\cup (B\cap C)\).

\(A,B\) and \(C\) are three sets. Prove that if we take an intersection \(A\cap B\) and unite it with the set \(C\), we will get the same set as if we took an intersection of two unions \(A\cup C\) and \(B\cup C\). Essentially, prove that \((A\cap B)\cup C = (A\cup C)\cap (B\cup C)\). Draw a Venn diagram for the set \((A\cap B)\cup C\).

Let \(A,B\) and \(C\) be three sets. Prove that if we take an intersection \(A\cap B\) and intersect it with the set \(C\), we will get the same set as if we took an intersection of \(A\) with \(B\cap C\). Essentially, prove that it does not matter where to put the brackets in \((A\cap B)\cap C = A\cap (B\cap C)\). Draw a Venn diagram for the set \(A\cap B\cap C\).
Prove the same for the union \((A\cup B)\cup C = A\cup (B\cup C) = A\cup B\cup C\).

For three sets \(A,B,C\) prove that \(A - (B\cup C) = (A-B)\cap (A-C)\). Draw a Venn diagram for this set.