Problems

Is \(\text{Nim}(1,2,4,5,5)\) a winning position or a losing position?

When we write \(137\) in decimal, we mean \(1 \times 10^2 + 3 \times 10 + 7 \times 1\). If we write it instead using powers of \(2\), we have \(137 = 1 \times 2^7 + 0 \times 2^6 + 0 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 0 \times 2^1 + 1 \times 2^0\). To tell apart binary representation from decimals, we can use the following notation: \(137 = (10001001)_2\).

What is the number \(273\) in binary? Note that using binary is useful for finding whether a particular Nim game is a winning position or a losing position.

Let us define XOR (or addition mod 2). XOR is defined for 0 and 1 only. Here is a table recording the values of XOR:

Now we define the important concept of nim-sum. Given two natural numbers \(x\) and \(y\), we first convert them into binary representations and then compute XOR on individual digits. The resulting number, denoted \(x \oplus y\), is the nim-sum of \(x\) and \(y\). Here is an example.

This is simply saying \(22 \oplus 5 = 19\). Note that \(22=(10110)_2\) and \(5=(00101)_2\).

Verify \((x \oplus y) \oplus z = x \oplus (y \oplus z)\), so we can speak of \(x \oplus y \oplus z\) with no ambiguity.

Show that \(x \oplus y = 0\) if and only if \(x = y\). Remember that \(x \oplus y\) denotes the nim-sum of \(x\) and \(y\).

Suppose you have a coffee mug made of stretchy and expandable material. How do you mold it into a donut that has a hole inside?

Take a straight string of finite length. Put the right half on top of the left half to form a hoop, and then pass it (the piece now on top) through the hoop from underneath. Glue the two ends together to form the trefoil knot.

Draw a sequence of pictures to illustrate the formation of the trefoil knot.

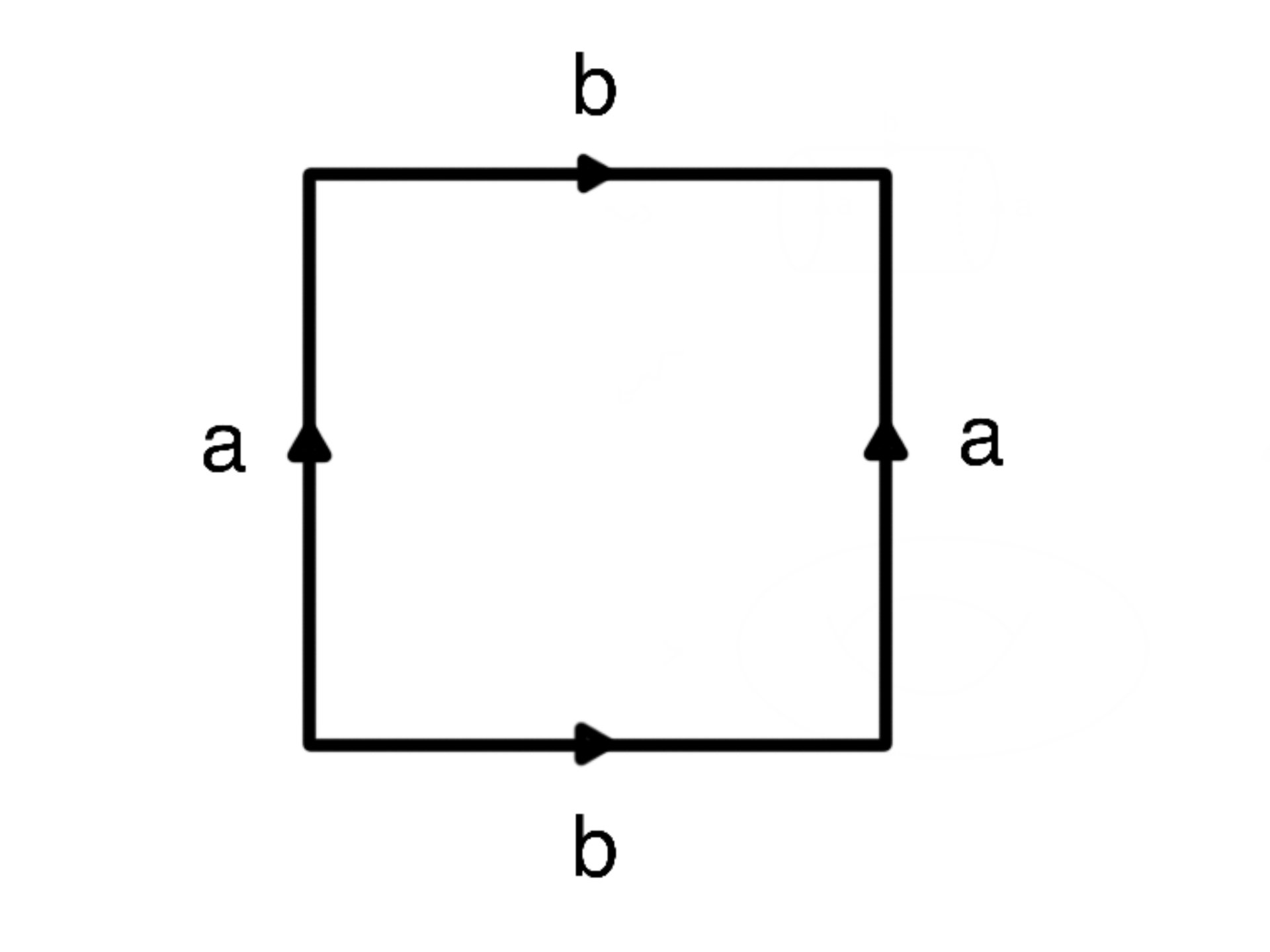
In the picture below, each side is glued in the same direction as its opposite side. Draw a sequence of pictures to show the gluing process and the final shape.

Take a straight string of finite length. Wrap the right half over and then under the left half so that it is pointing to the right again and there is a hoop. Pass the right pointing piece through the hoop from above. Glue the two ends together to form the figure-8 knot.

Draw a sequence of pictures to illustrate the formation of the figure-8 knot, seen below.

Explain why it is possible to have a picture of a figure-8 knot with 100 crossings.

The unknot is the simplest knot, formed by taking a piece of straight string and gluing its two ends together. In reality, there is no knot! Now, which of the following two knots is the unknot?

Show that a knot that can be drawn with only one crossing must be the unknot.