Problems
A restaurant offers \(5\) choices of starter, \(10\) choices of the main course, and \(4\) choices of dessert. A customer can choose to eat just one course, or two different courses, or all three courses. Assuming that all food choices are available, how many different possible meals does the restaurant offer?
Find how many \(5\)-digit numbers contain only one \(0\) and one \(1\) in their decimal representation
Given a pile of cards, is it true that reversing the order of the pile by counting the cards out one by one leaves no card in its original position?
How many permutations of \(13\) cards swap the third card and the fourth card?
Consider lifting the top \(2\) cards from a pile of \(6\) cards and placing them at the bottom of the pile. Show how the same process can be done by switching adjacent pairs of cards.
Lennart is a skilled magician - he can shuffle a deck of card in the most arbitrary ways and replicate the shuffle. Once he performed a terribly complicated shuffle and repeated it right away. It turned out all the cards returned to their original position. Show that this complicated shuffle consists of only switching distinct pairs of cards (or keeping some cards where they are).
Take Ace to King of any one suit to make a pile. The cards are in numerical order, so that Ace is at the top and King is at the bottom. Count out four cards from the top one by one and put the rest of the pile on top of the four cards.
If you perform this action a total of \(7\) times, what is now the top card?
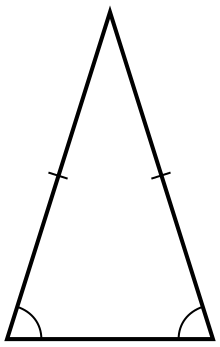
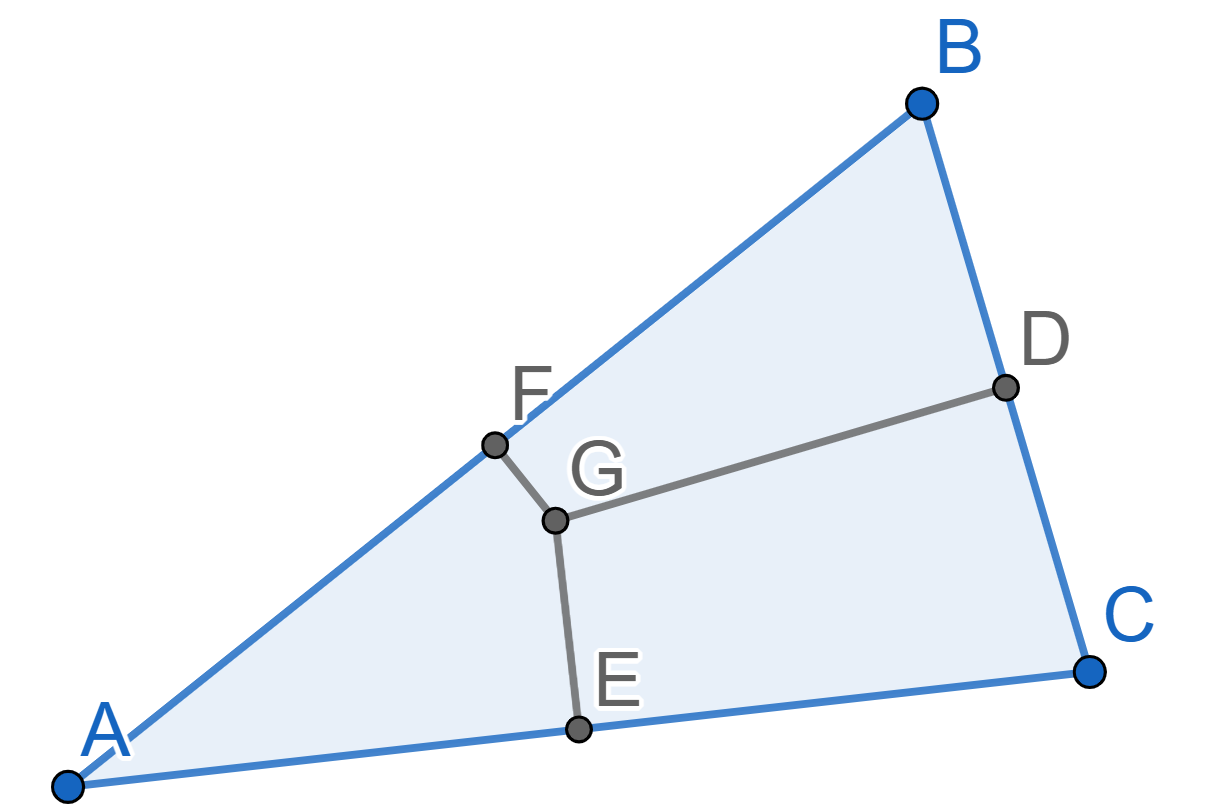
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Prove that the perpendicular bisectors to the sides \(AB\), \(BC\), \(AC\) intersect at one point.
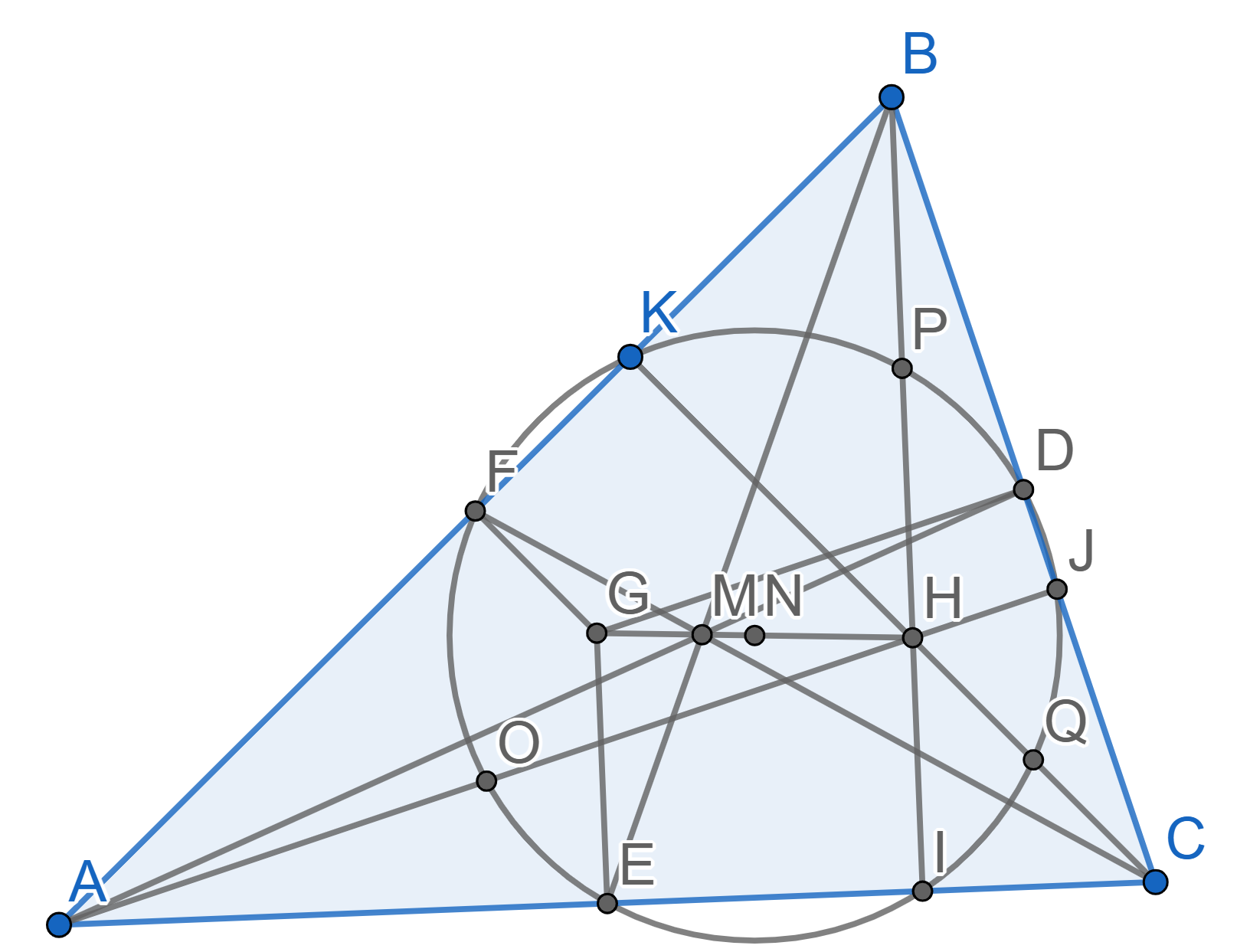
Let \(ABC\) be a triangle with midpoints \(D\) on the side \(BC\), \(E\) on the side \(AC\), and \(F\) on the side \(AB\). Let \(M\) be the point of intersection of all medians of the triangle \(ABC\), let \(H\) be the point of intersection of the heights \(AJ\), \(BI\) and \(CK\). Prove that the points \(D\), \(J\), \(I\), \(E\), \(F\) and \(K\) all lie on one circle.