Problems
What are the symmetries of an equilateral triangle?
What are the symmetries of a rectangle (which is not a square)?
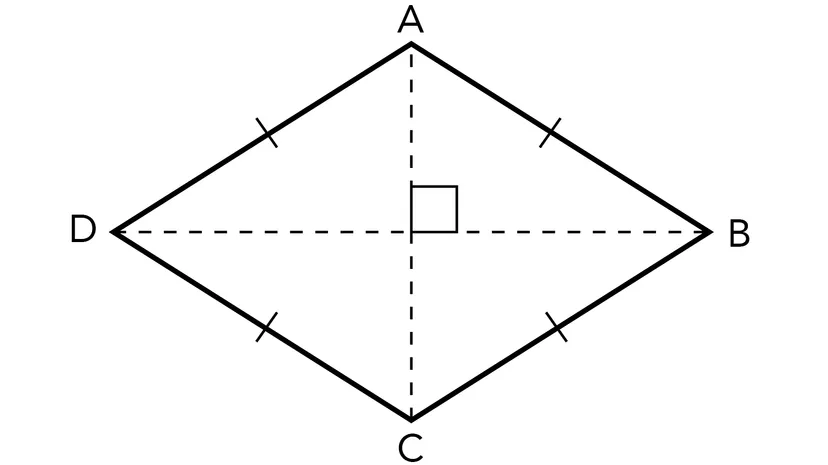
What are the symmetries of a rhombus (which isn’t a square)?
Take a pile of cards, Ace to 7 of Diamonds. Consider the following shuffle: simultaneously move the first card to the third position, the third card to the fifth position, the fifth card to the seventh position, and the seventh card to the first position. Also move the second card to the fourth position, the fourth card to the sixth position and the sixth card to the second position.
How many times do you have to do this one specific shuffle in a row to get back to where you started?
How many permutations are there of 4 cards leaving no card in the same position as before?
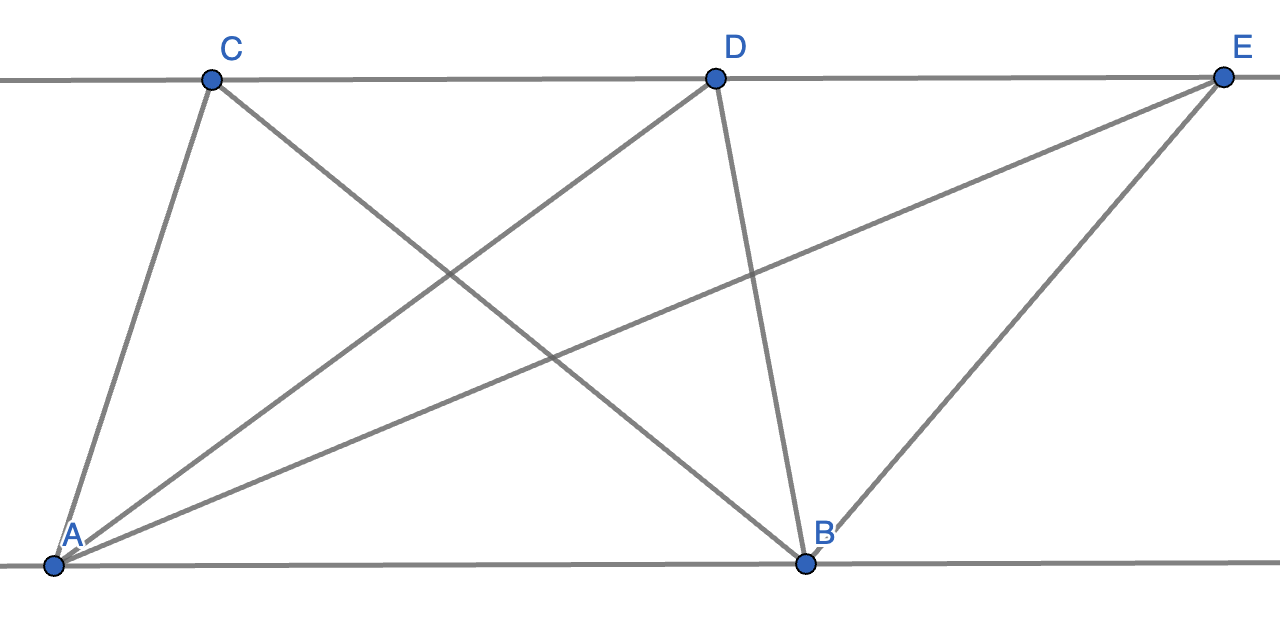
Lines \(AB\) and \(CDE\) are parallel. Which triangle out of \(\triangle ABC\), \(\triangle ABD\) and \(\triangle ABE\) has the greatest area?
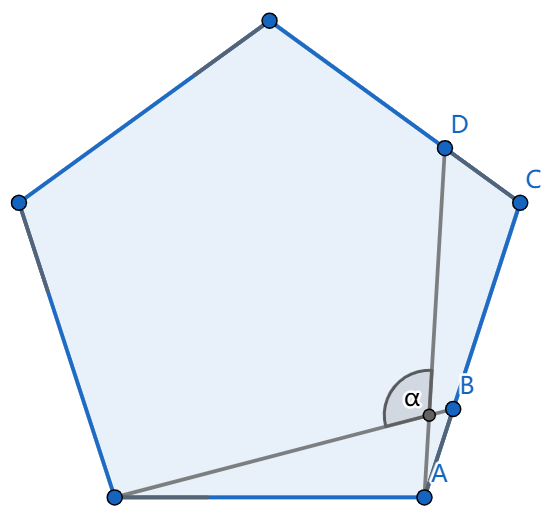
In the picture below, we have a regular pentagon. The segments \(AB\) and \(CD\) have equal lengths. What is the angle \(\alpha\)?
We have two squares sharing the same centre, each with side length \(2\). Show that the area of overlap is at least \(3\).