Problems

How many independent queens can you place on a \(5\times5\) grid? That is, so none of them attack each other.

How many ways can you place \(8\) rooks independently on a chessboard? That is, so that none of them attack each other.

Why are there no closed knight’s tours on an \(n\times n\) grid when \(n\) is odd? A knight’s tour is closed if you can get to the first square from the last square by a knight’s move.

Show how to place fourteen dominating bishops on a standard \(8\times8\) chessboard. That is, every square either contains a bishop, or is attacked by some bishop.

Place eight independent queens on a standard \(8\times8\) chessboard.

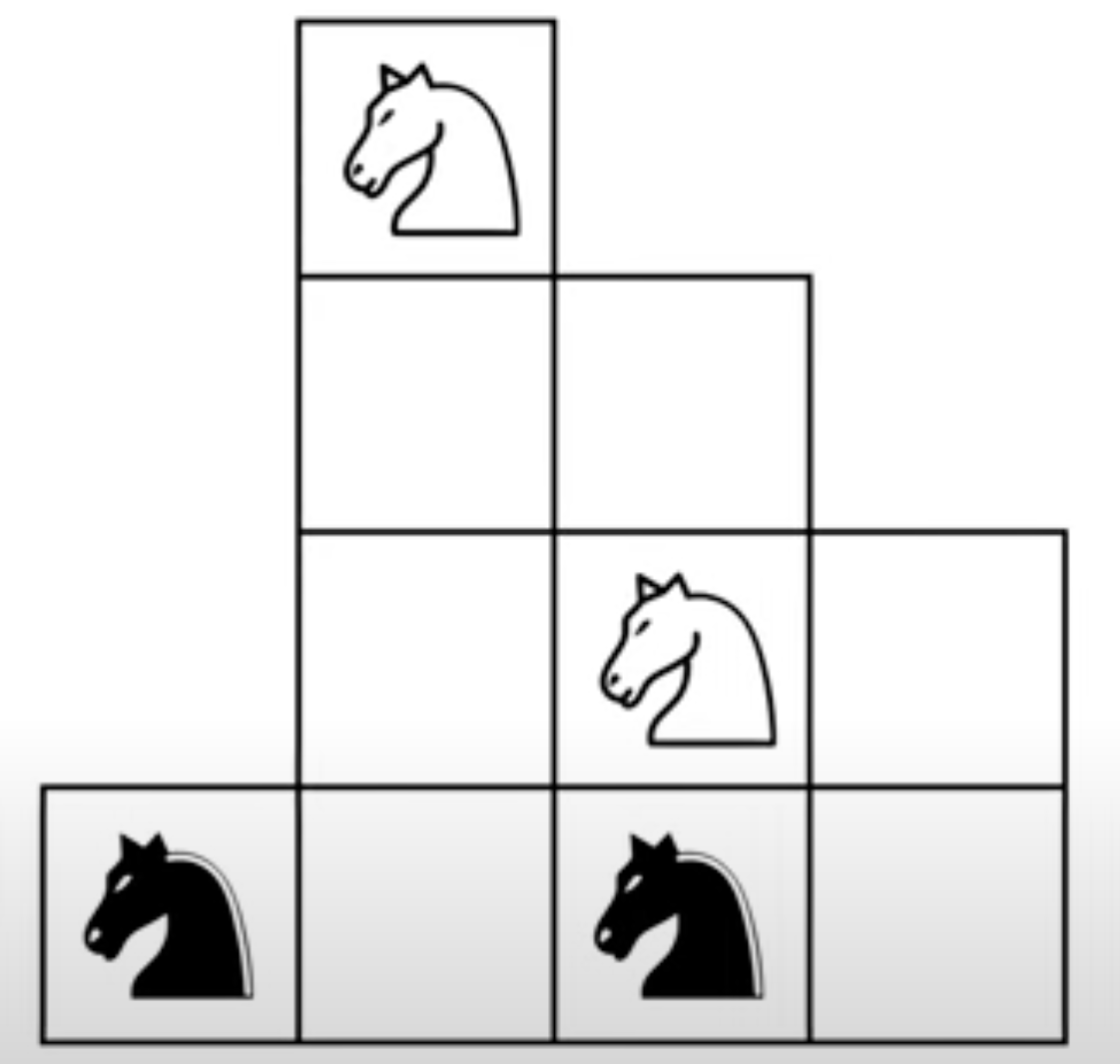
Show how to swap the two pairs of knights on the following strangely-shaped grid. That is, the knights make one move at a time, and you’re trying to get the black nights to where the white knights are, and the white knights to where the black knights are.

Let \(n\) be a positive integer. Prove that it’s impossible to have a closed knight’s tour on a \(4\times n\) grid.

Find an open knight’s tour on a \(2\times2\times2\) cube.

Let \(s\) and \(t\) be two positive integers. Can we have \(s^2=t^2+2\)?

Prove Sperner’s lemma in dimension \(1\), namely on a line.
The simplex in this case is just a segment, the triangulation is subdivision of the segment into multiple small segments, and the conditions of a Sperner’s coloring are the following:

• There are only two colors;

• The opposite ends of the main segment are colored differently;

Then one needs to prove that there exists a small segment with two ends colored in different colors. In particular there is an odd number of such small segments.