Problems

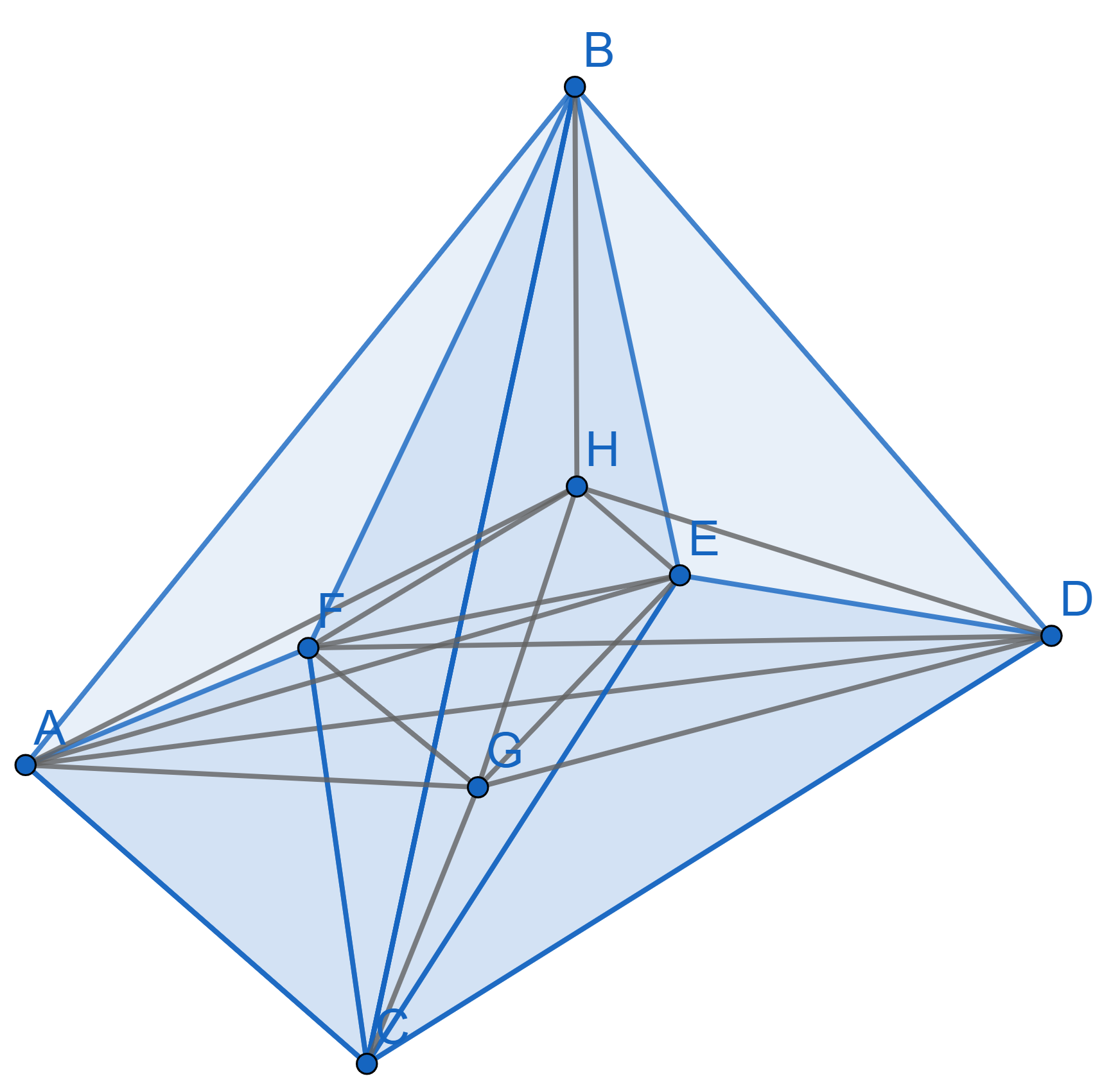
Draw a Sperner’s coloring for the following \(3\)-dimensional simplex. The blue segments are visible, the grey ones are inside the tetrahedron. The point \(F\) is on the face \(ABC\), point \(E\) is on the face \(BCD\), point \(G\) is on the face \(ACD\) and the point \(H\) is on the face \(ABD\).

Four football teams play in a tournament. There’s the Ulams (\(U\)), the Vandermondes (\(V\)), the Wittgensteins (\(W\)) and the Xenos (\(X\)). Each team plays every other team exactly once, and matches can end in a draw.
If a game ends in a draw, then both teams get \(1\) point. Otherwise, the winning team gets \(3\) points and the losing team gets \(0\) points. At the end of the tournament, the teams have the following points totals: \(U\) has \(7\), \(V\) has \(4\), \(W\) has \(3\) and \(X\) has \(2\).

Work out the results of each match, including showing that there’s no other way the results could have played out.

Imagine a \(5\times6\) rectangular chocolate bar, and you want to split it between you and your \(29\) closest friends, so that each person gets one square. You repeatedly snap the chocolate bar along the grid lines until the rectangle is in \(30\) individual squares. You can’t snap more than one rectangle at a time.

The diagram shows a couple of choices for your first two snaps. For example, in the first picture, you snap along a vertical line, and then snap the left rectangle along a horizontal line.
How many snaps do you need to get the \(30\) squares?

Prove that \(n^{n+1}>(n+1)^n\) for integers \(n\ge3\).

What is the following as a single fraction? \[\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+...+\frac{1}{98\times99}+\frac{1}{99\times100}.\]

Prove that \(3\) always divides \(2^{2n}-1\), where \(n\) is a positive integer.

Adi and Maxim play a game. There are \(100\) sweets in a bowl, and they each take in turns to take either \(2\), \(3\) or \(4\) sweets. Whoever cannot take any more sweets (since the bowl is empty, or there’s only \(1\) left) loses.

Maxim goes first - who has the winning strategy?

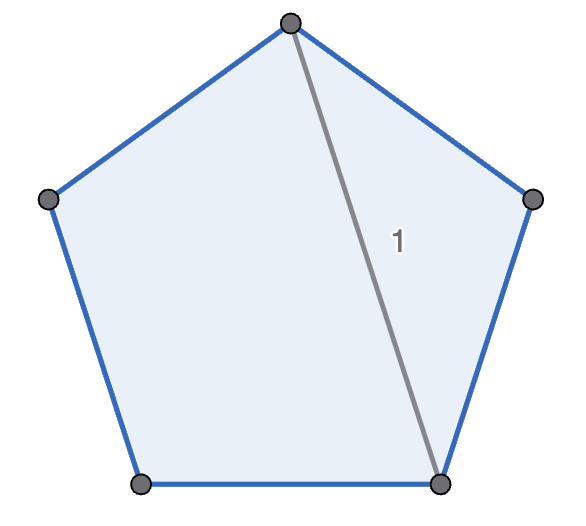
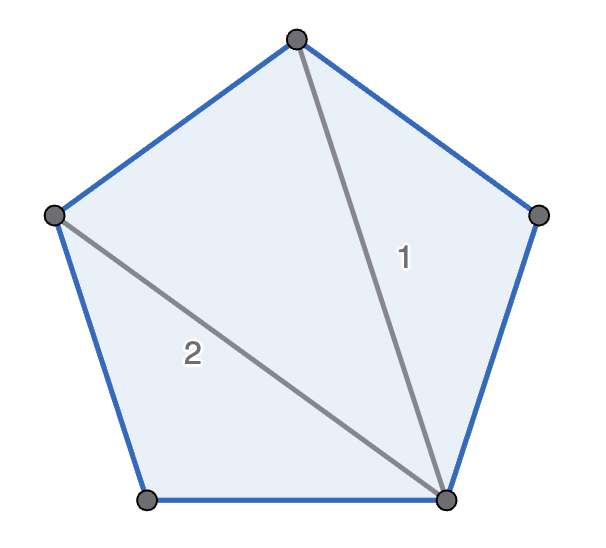
Michelle and Mondo play the following game, with Michelle going first. They start with a regular polygon, and take it in turns to move. A move is to pick two non-adjacent points in one polygon, connect them, and split that polygon into two new polygons. A player wins if their opponent cannot move - which happens if there are only triangles left. See the diagram below for an example game with a pentagon. Prove that Michelle has the winning strategy if they start with a decagon (\(10\)-sided polygon).

Let \(n\) be a positive integer. Show that \(1+3+3^2+...+3^{n-1}+3^n=\frac{3^{n+1}-1}{2}\).

Show that all integers greater than or equal to \(8\) can be written as a sum of some \(3\)s and \(5\)s. e.g. \(11=3+3+5\). Note that there’s no way to write \(7\) in such a way.