Problems

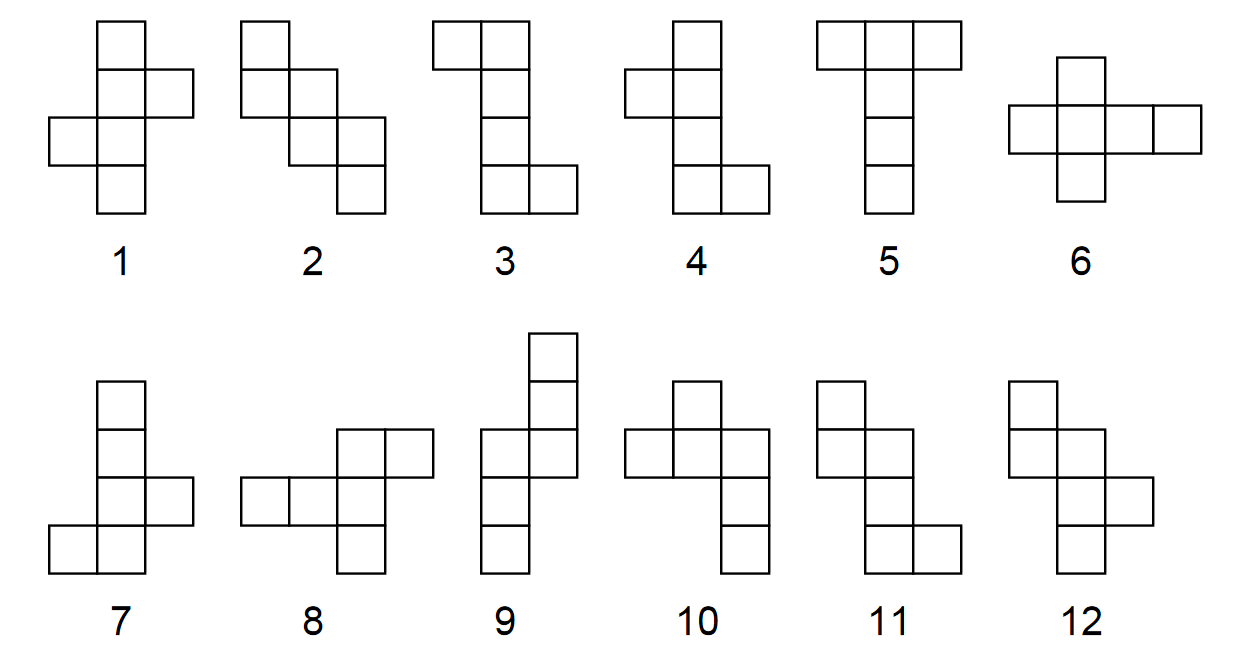
David Smith cut out 12 nets. He claimed that it was possible to make a cube out of each net. Roger Penrose looked at the patterns, and after some considerable thought decided that he was able to make cubes from all the nets except one. Can you figure out which net cannot make a cube?

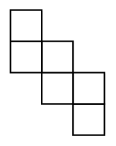
It is known that it is possible to cover the plane with any cube’s net. Show how you can cover the plane with this net:

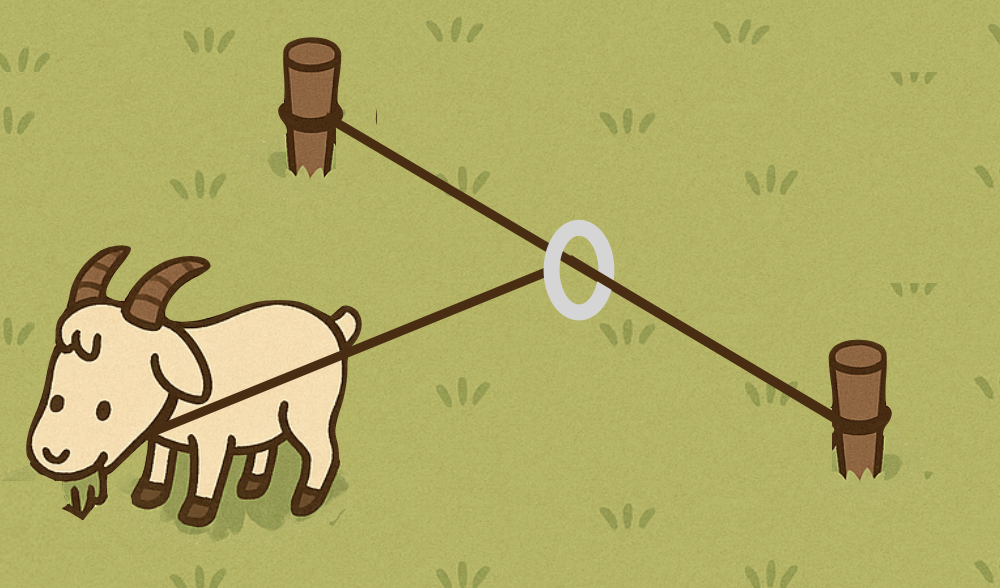
One day, Robinson Crusoe tied a rope tightly between two pegs, placed a sliding ring on it, and then tied the goat to the ring with another rope, as in the picture below. What shape did the goat graze this time?

On another day, Robinson Crusoe used two pegs again. This time, he tied one rope of length \(a\) to the first peg and another rope of length \(b\) to the second peg, both directly to the goat, so that it looked like in the picture below. What shape did the goat graze that day?

One day Robinson Crusoe went for a walk on a plateau, taking his goat with him on a rope of length one meter. He walked along a path in the shape of a rectangle measuring \(1 \,\text{km} \times 3 \,\text{km}\), following its perimeter. What was the shape of the area where the goat could graze while walking with Robinson?

Draw how Robinson Crusoe should use pegs, ropes, and sliding rings to tie his goat in order for the goat to graze grass in the shape of a semicircle.

Can two tied wolves keep an untied goat in a triangle?

Prove the divisibility rule for \(3\): a number is divisible by \(3\) if and only if the sum of its digits is divisible by \(3\).

While studying numbers and their properties, Robinson came across a three-digit prime number whose last digit equals the sum of the first two digits. What are the options for the last digit of this number, given that none of its digits is zero?

Prove the divisibility rule for \(4\): a number is divisible by \(4\) if and only if the number made by the last two digits of the original number is divisible by \(4\);
Can you come up with a divisibility rule for \(8\)?