Problems

What is the smallest positive whole number whose digits add up to \(2026\)?

The thirteen dwarves sat down around a bonfire in a circle, and their leader Thorin proposed a challenge to pass the time:

Each dwarf would choose an integer (it is not necessary that each dwarf chooses a different number) so that for every group of three neighboring dwarves, the sum of their numbers must be exactly \(13\).

Does Thorin’s challenge have a solution?

In the month of January of a certain year, there are exactly \(4\) Mondays and \(4\) Fridays. What day of the week is the \(20^{\text{th}}\) day of this month?

Which of the two following numbers is larger: \(31^{11}\) or \(17^{14}\)?

Zippity the robot speaks a language of \(n\) words which can be written with \(0\)s and \(1\)s. In this language, no word appears as the first several digits of another word. For example: if “\(1001\)” is a word, then “\(100101\)” can’t be a word. Show that if \(\ell_1,\cdots, \ell_n\) are the lengths of each word (i.e: the number of digits), then \[\frac{1}{2^{\ell_1}}+\frac{1}{2^{\ell_2}}+\cdots + \frac{1}{2^{\ell_n}}\leq 1.\]

Prove that under a homothety transformation, a circle is transformed into another circle. Consider all possible cases of \(k\): \(k<0, 0<k \leq 1, 1\leq k\).

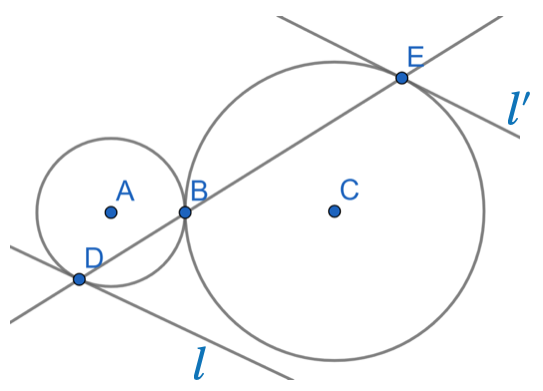
Two circles with centres \(A\) and \(C\) are tangent at the point \(B\). The segment \(DE\) passes through the point \(B\). Prove that the tangent lines \(l\) and \(l'\) passing through the points \(D\) and \(E\) respectively, are parallel.

Let \(ABCD\) be a square, a point \(I\) a random point on the plane. Consider the four points, symmetric to \(I\) with respect to the midpoints of \(AB, BC, CD, AD\). Prove that these new four points are vertices of a square.
In case you need a refresher, we say that a point \(X'\) is symmetric to a point \(X\) with respect to a point \(M\) if \(M\) is the midpoint of the segment \(XX'\).

At the Oscar Awards 2025, 5 films were nominated for Best Production Design and 5 films were nominated for Best Cinematography. In fact, 3 films were nominated for both categories. What is the total number of films nominated for these two categories?

150 young adults were asked how they commuted to work. 125 said they took the underground and 93 said they cycled. Of all the people interviewed, 72 said they both cycled and took the underground. How many people do not cycle and do not take the underground?