Problems
Show that there are no more than 269 prime numbers less than or equal to 1000.
200 people were asked if they drank one of the following beverages regularly: tea, coffee and beer. 165 people said they drank at least one of these beverages. Funnily, for every choice of a pair of beverages, exactly 122 people said they drank at least one beverage out of the pair. The even stranger fact was that for each choice of a beverage, exactly 73 people admitted to drinking it.
How many people drink all three beverages?
Each student chooses at least one from the \(n\) different modules offered at a university. Let us number these modules as \(1,2,3,\dots,n\). For each natural number \(1\leq k\leq n\), we denote the number of students choosing the modules \(i_1,\dots,i_k\) by \(S(i_1,\dots,i_k)\). Give a formula for the number of students in terms of the numbers \(S(i_1,\dots,i_k)\).
As an example, if \(n = 5\), \(k=3\) and we look at \(i_1 = 4,i_2 = 2, i_3 =1\), then \(S(i_1,i_2,i_3) = S(4,2,1)\) is the number of students picking the modules \(1,2,4\).
There are \(n\) seats on a plane and each of the \(n\) passengers sat in the wrong seat. What is the total number of ways this could happen?
Let \(n\geq 2\) be an integer. Fix \(2n\) points in space, so that no four points lie on a common plane. Suppose there are \(n^2+1\) segments between these points. Show that these segments must form at least \(n\) triangles.
Three kinds of cookies are sold at a store: dark chocolate \((D)\), raspberry with white chocolate \((R)\) and honeycomb \((H)\). Here is a table summarizing the number of people buying cookies this morning.
| \(D\) | \(R\) | \(H\) | \(D, R\) | \(D,H\) | \(R,H\) | \(D,R,H\) | |
|---|---|---|---|---|---|---|---|
| Number of people | 16 | 16 | 10 | 7 | 5 | 3 | 1 |
The column with label \(D,H\), for example, means the number of people who bought both dark chocolate and honeycomb cookies.
How many people bought cookies this morning?
We write all \(26\) different letters of the English alphabet in a line, using each letter exactly once.
How many such arrangements do not contain any of the strings
fish, rat, or bird?
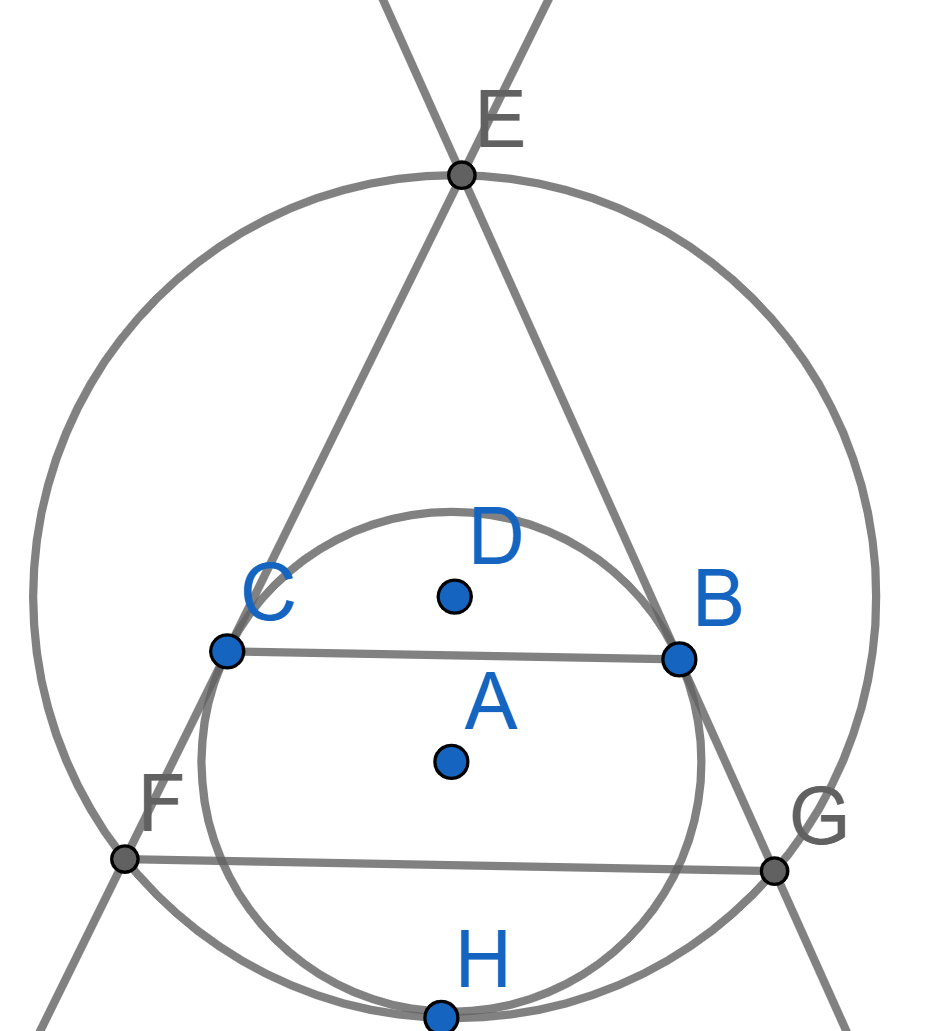
The triangle \(EFG\) is isosceles with \(EF=EG\). A circle with center \(A\) is tangent to the sides \(EF\) and \(EG\) at the points \(C\) and \(B\) respectively. It is also tangent to the circle circumscribed around the triangle \(EFG\) at the point \(H\). Prove that the midpoint of the segment \(BC\) is the center of the circle inscribed into the triangle \(EFG\).
Prove that under a homothety transformation, a polygon is transformed into a similar polygon.
Hint: to show this, why is it enough for you to show that homothety preserves angles and ratios?
In the Game of Life, each cell in a grid is either alive or dead (in the diagram, yellow cells are alive). At each step, a live cell stays alive only if it has \(2\) or \(3\) live neighbours, otherwise it dies; a dead cell becomes alive only if it has exactly \(3\) live neighbours. A still-life is a pattern that does not change after any number of steps. Show that the following pattern cannot be turned into a still-life by only changing dead cells into alive cells.
