We solve problems

Problem #PRU-103885

Problems Discrete Mathematics Combinatorics Dissections, partitions, covers and tilings Tilings with ordinary and domino tiles

11–12 2.0

At the disposal of a tile layer there are 10 identical tiles, each of which consists of 4 squares and has the shape of the letter L (all tiles are oriented the same way). Can he make a rectangle with a size of \(5 \times 8\)? (The tiles can be rotated, but you cannot turn them over). For example, the figure shows the wrong solution: the shaded tile is incorrectly oriented.

Problem #PRU-103887

Problems Discrete Mathematics Set theory and logic Mathematical logic Puzzles Algebra Fractions Simple fractions

12–12 2.0

Arrange brackets and arithmetic signs around these numbers so that the correct equality is obtained: \[\frac{1}{2}\quad \frac{1}{6}\quad \frac{1}{6009} \ = \ 2003.\]

Problem #PRU-103888

Problems Methods Algebraic methods Proof by exhaustion Geometry Solid geometry Visual geometry in space

11–12 2.0

A square napkin was folded in half, the resulting rectangle was then folded in half again (see the figure). The resulting square was then cut with scissors (in a straight line). Could the napkin have been broken up a) into 2 parts? b) into 3 parts? c) into 4 parts? d) into 5 parts? If yes – illustrate such a cut, if not – write the word “no”.

Problem #PRU-103899

Problems Discrete Mathematics Combinatorics Discrete geometry (other)

12–12 2.0

A rabbit, preparing for the arrival of guests, hung lightbulbs in three corners of his polygonal hole. Winnie the Pooh and Piglet came and noticed that lights did not illuminate all the pots of honey which were in the rabbit hole. When they reached for some honey, two of the lightbulbs broke. The rabbit moved the remaining light bulb into some corner so that the whole hole was lit up. Is this possible? (If yes, draw an example, if not, justify the answer.)

Problem #PRU-103946

Problems Number Theory Arithmetic operations. Number identities

11–12 2.0

The number \(A\) is positive, \(B\) is negative, and \(C\) is zero. What is the sign of the number \(AB + AC + BC\)?

Problem #PRU-103947

Problems Geometry Plane geometry Area

10–12 2.0

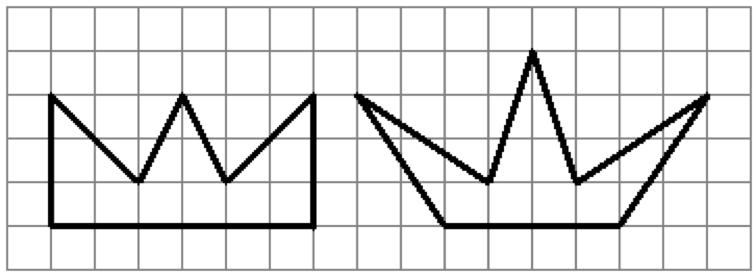
Find the area of the figures shown below.

Problem #PRU-103955

Problems Discrete Mathematics Algorithm Theory Game theory Winning and loosing positions

12–13 2.0

Ben and Joe play chess. In addition to a chessboard, they have one rook, which they put in the lower right corner, and they move it in turns. It can only be moved upwards or to the left (for any number of cells). The player who can not make a move, loses. Joe goes first. Who will win with the correct method?

Problem #PRU-103960

Problems Methods Pigeonhole principle Pigeonhole principle (other)

11–13 2.0

Prove that if 21 people collected 200 nuts between them, there are two people in the group who collected the same number of nuts.

Problem #PRU-103966

Problems Algebra Algebraic equations and systems of equations Higher order equations. Palindromic polynomial equations Equations of higher order (other) Calculus Real numbers Integer and fractional parts. Archimedean property

12–14 2.0

In Mongolia there are in circulation coins of 3 and 5 tugriks. An entrance ticket to the central park costs 4 tugriks. One day before the opening of the park, a line of 200 visitors queued up in front of the ticket booth. Each of them, as well as the cashier, has exactly 22 tugriks. Prove that all of the visitors will be able to buy a ticket in the order of the queue.

Problem #PRU-103967

Problems Discrete Mathematics Algorithm Theory Theory of algorithms (other)

10–12 2.0

There is a rectangular table. Two players start in turn to place on it one pound coin each, so that these coins do not overlap one another. The player who cannot make a move loses. Who will win with the correct strategy?