Problems
The bank of the Nile was approached by a group of six people: three Bedouins, each with his wife. At the shore is a boat with oars, which can withstand only two people at a time. A Bedouin can not allow his wife to be without him whilst in the company of another man. Can the whole group cross to the other side?
Is it possible for the mean of some 35 whole numbers to equal \(6.35\)?
Is it possible to place 12 identical coins along the edges of a square box so that touching each edge there were exactly: a) 2 coins, b) 3 coins, c) 4 coins, d) 5 coins, e) 6 coins, f) 7 coins.
You are allowed to place coins on top of one another. In the cases where it is possible, draw how this could be done. In the other cases, prove that doing so is impossible.
A field that will be used to grow wheat has a rectangular shape. This year, the farmer responsible for this field decided to increase the length of one of the sides by \(20\%\) and decrease the length of another side by \(20\%\). The field remains rectangular. Will the harvest of wheat change this year and, if so, then by how much?
Solve problem number 108736 for the inscription \(A\), \(BC\), \(DEF\), \(CGH\), \(CBE\), \(EKG\).
At the end of the term, Billy wrote out his current singing marks in a row and put a multiplication sign between some of them. The product of the resulting numbers turned out to be equal to 2007. What is Billy’s term mark for singing? (The marks that he can get are between 2 and 5, where 5 is the highest mark).
Replace \(a, b\) and \(c\) with integers not equal to \(1\) in the equality \((ay^b)^c = - 64y^6\), so it would become an identity.
Sarah believes that two watermelons are heavier than three melons, Anna believes that three watermelons are heavier than four melons. It is known that one of the girls is right, and the other is mistaken. Is it true that 12 watermelons are heavier than 18 melons? (It is believed that all watermelons weigh the same and all melons weigh the same.)
Prove that for all \(x \in (0;\pi /2)\) for \(n > m\), where \(n, m\) are natural, we have the inequality \(2 | \sin^n x-\cos^n x | \leq 3 | \sin^m x-\cos^m x |\);
Members of the State parliament formed factions in such a way that for any two factions \(A\) and \(B\) (not necessarily different)
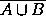
– also a faction (through
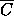
the set of all parliament members not included in \(C\) is denoted). Prove that for any two factions \(A\) and \(B\), \(A \cup % \includegraphics{https://problems-static.s3.amazonaws.com/production/problem_images/109909-3.png} B\) is also a faction.