Problems
For two congruent triangles Prove that their corresponding heights are equal.
The sides \(AB\) and \(CD\) of the quadrilateral \(ABCD\) are equal, the points \(E\) and \(F\) are the midpoints of \(AB\) and \(CD\) correspondingly. Prove that the
perpendicular bisectors of the segments \(BC\), \(AD\), and \(EF\) intersect at one point.
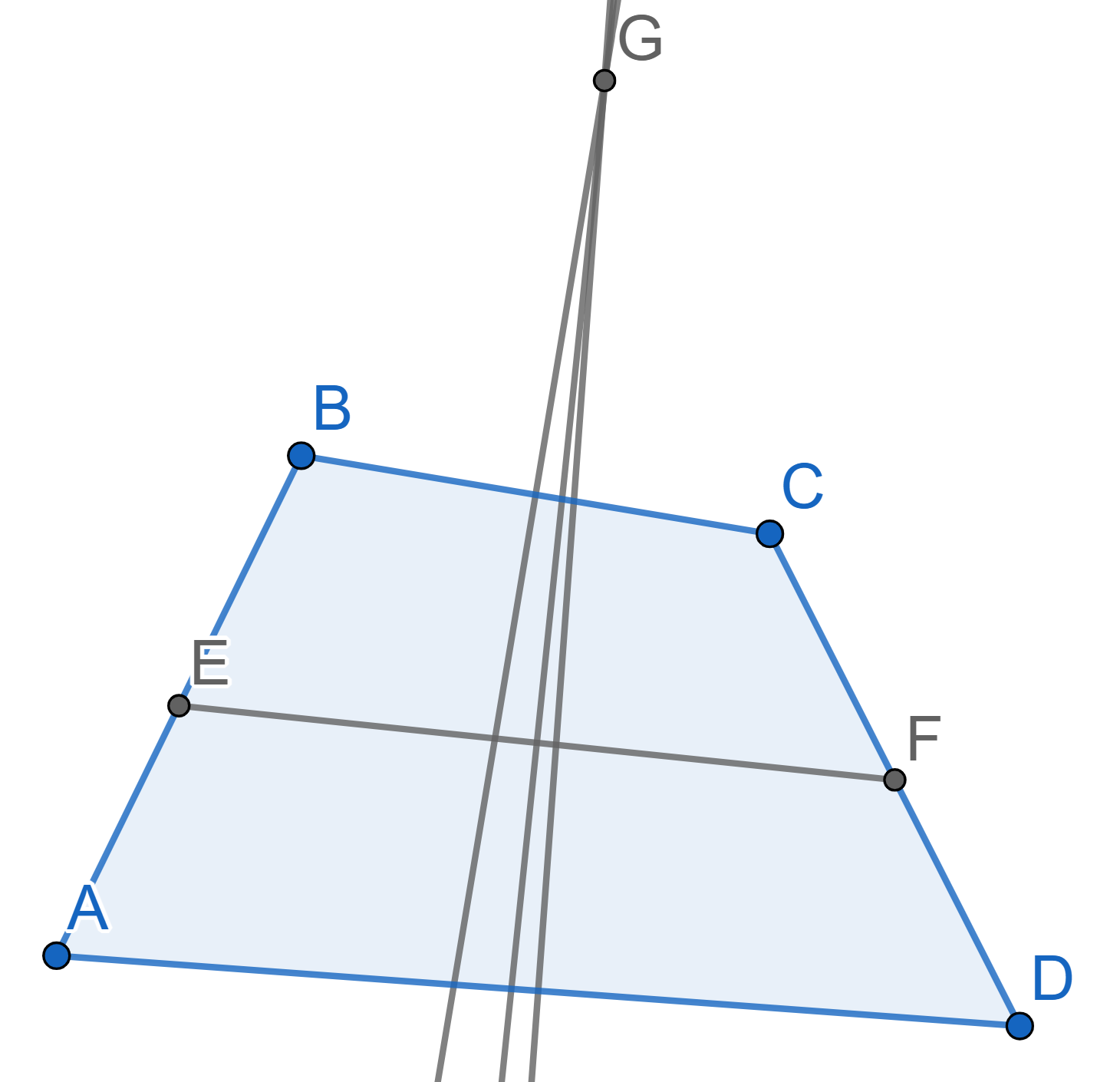
In the triangle \(ABC\) the heights \(AD\) and \(CE\) intersect at the point \(F\). It is known that \(CF=AF\). Prove that the triangle \(ABC\) is isosceles.
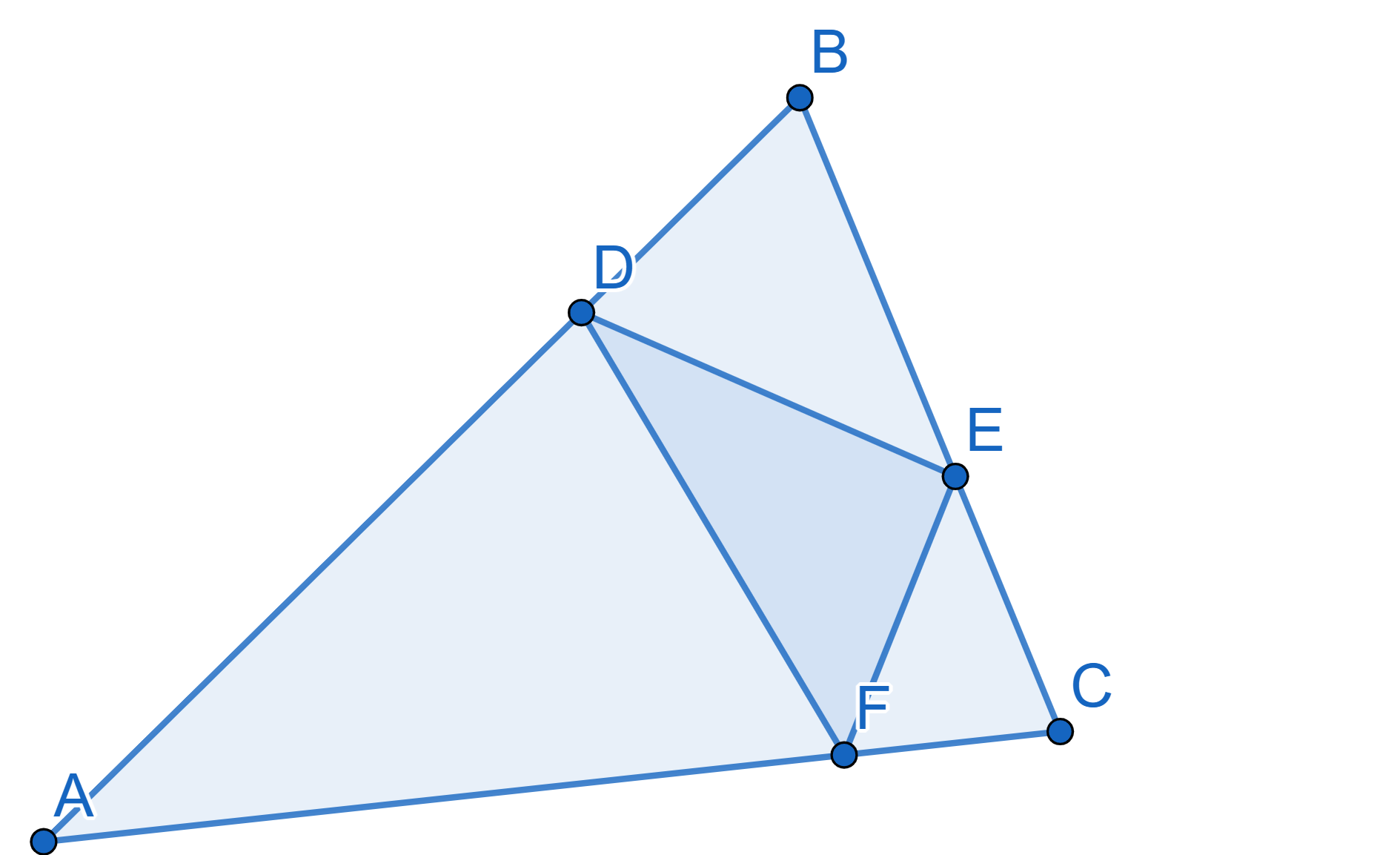
In the triangle \(ABC\) the points
\(D,E,F\) are chosen on the sides \(AB, BC, AC\) in such a way that \(\angle ADF = \angle BDE\), \(\angle AFD = \angle CFE\), \(\angle CEF = \angle BED\). Prove that the
segments \(AE, BF, CD\) are the heights
of the triangle \(ABC\).
There are real numbers written on each square of an \(m \times n\) chessboard. Some of them are negative, some are positive. In one move we can multiply all the numbers in one column or row by \(-1\). Is that always possible to obtain a chessboard where sums of numbers in each row and column are non-negative?
Tom found a large, old clock face and put \(12\) sweets on the number \(12\). Then he started to play a game: in each move he moves one sweet to the next number clockwise, and some other to the next number anticlockwise. Is it possible that after finite number of steps there is exactly \(1\) of the sweets on each number?
The numbers \(1,2,3,4,5,6,7,8,9\) and \(10\) are written on a board.
In one move, you may erase any three of the remaining numbers, call them \(a,b\) and \(c\), and replace them with the three numbers \(2a+b,\; 2b+c\) and \(2c+a\).
Is it possible, after a sequence of such moves, for all \(10\) numbers on the board to be equal?
On a certain island there are \(17\) grey, \(15\) brown and \(13\) crimson chameleons. If two chameleons of different colours meet, then both of them change into the third colour. No other colour changes are allowed. Is it possible that, after a number of such colour changes, all the chameleons have the same colour?
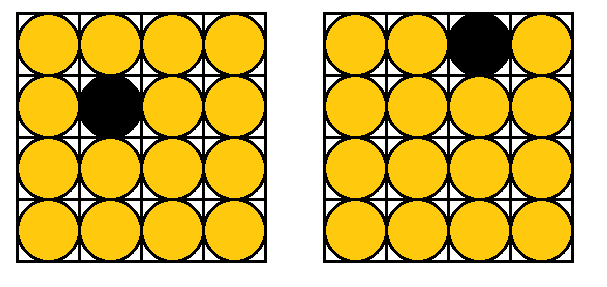
Sixteen lightbulbs are arranged in a \(4 \times 4\) grid. Some of them are on, the other ones are off. You are allowed to change the state of all the bulbs in a column, in a row, or along any diagonal (note: there are \(14\) diagonals in total!). Is it possible to go from the arrangement on the left to the one on the right by repeating this operation?
The numbers \(1\) to \(2025\) are written on a board. In one move, we may erase any two numbers and replace them with the absolute value of their difference. Can we, after some number of moves, end up with a sequence consisting only of \(0\)?