Problems

Sixteen lightbulbs are arranged in a \(4 \times 4\) grid. Some of them are on, the other ones are off. You are allowed to change the state of all the bulbs in a column, in a row, or along any diagonal (note: there are \(14\) diagonals in total!). Is it possible to go from the arrangement on the left to the one on the right by repeating this operation?

The numbers \(1\) to \(2025\) are written on a board. In one move we can erase two numbers and replace them with the absolute value of their difference. Can we achieve a sequence consisting of only \(0\) after some number of moves?

In the quadrilateral \(ABCD\) the diagonals \(AC\) and \(BD\) intersect at the point \(E\). It is known that the perimeter of the triangle \(ABC\) is equal to the perimeter of the triangle \(ABD\), and the perimeter of the triangle \(ACD\) equals the perimeter of the triangle \(BCD\).

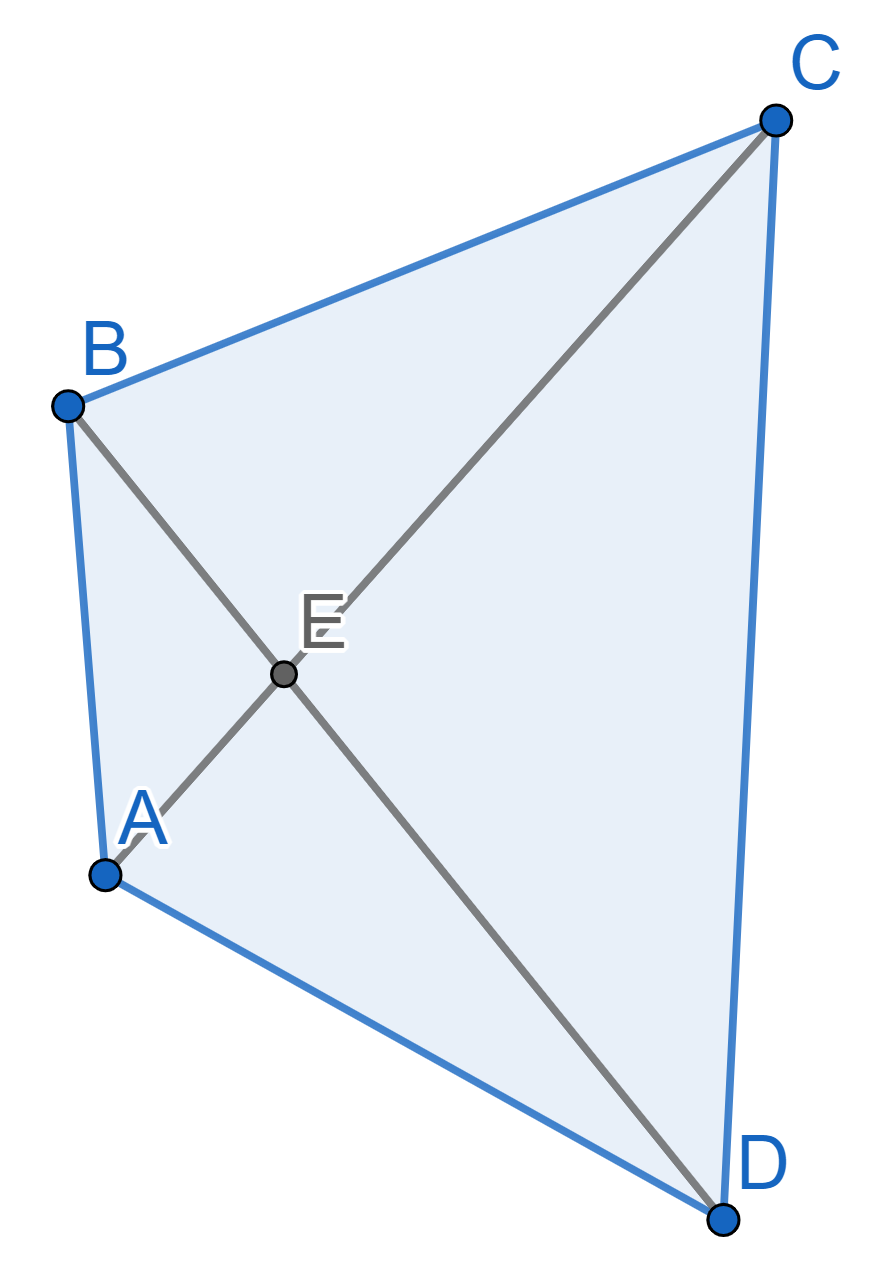
Prove that \(AE=BE\).

A magic square is a square filled with numbers, one in each cell, in such a way that the sums of the numbers in each row, each column and along each of the two main diagonals are the same. The value of this sum is known as the magic constant of the square. Show that in any \(4 \times 4\) magic square (which contains \(16\) numbers) the sum of all the numbers in the \(4\) central squares is also equal to the magic constant of the square.

Show that for any natural number \(n\geq 1\), the number \[n^4+4n^2+9\] is not a perfect square.

There are \(12\) light bulbs placed on top of the numbers on a clock face. Initially, only the bulb at \(12\) is on. We can choose any \(6\) consecutive bulbs and change their state simultaneously, that is, if any were on, we turn them off, if any were off, we turn them on. Can we perform this operation multiple times so that in the end only the bulb at \(11\) is on?

A group of schoolboys are going to walk down a narrow path in a straight line, one behind the other. There are \(11\) boys, and among them are Will, Tom, and Alex. If exactly two of them walk directly next to each other, they will start arguing. But if the three of them are all next to each other, in any order, the third one will always break the argument of the other two. We don’t want any arguments to persist. How many ways are there to order all \(11\) boys?

For a natural number \(n\) consider a regular \(2n\)-gon, with every vertex coloured either blue or green. It is known that the number of blue vertices equals the number of green vertices. Show that the number of main diagonals (passing through the centre of the \(2n\)-gon) with both ends blue is the same as the number of main diagonals with both ends green.

A \(7 \times 7\) square was tiled using \(1 \times 3\) rectangular blocks in such a way that one of the squares has not been covered. Find all the squares that could be left without being covered.

On a \(9\times 9\) board \(65\) bugs are placed in the centers of some of the squares. The bugs start moving at the same time and speed to a square that shares a side with the one they were in. When they reach the center of that square, they make a \(90\) degrees turn and keep walking (without leaving the board). Prove that at some moment of time there are two bugs in the same square. Note: When they turn it can be either to the right or to the left.