Problems

On an \(8\times 8\) board there is a lamp in every square. Initially every lamp is turned off. In a move we choose a lamp and a direction (it can be the vertical direction or the horizontal one) and change the state of that lamp and all its neighbours in that direction. After a certain number of moves, there is exactly one lamp turned on. Find all the possible positions of that lamp.

Given a natural number \(n\) you are allowed to perform two operations: "double up", namely get \(2n\) from \(n\), and "increase by \(1\)", i.e. to get \(n+1\) from \(n\). Find the smallest amount of operations one needs to perform to get the number \(n\) from \(1\).

A set includes weights weighing \(1\) gram, \(2\) grams, \(4\) grams, ... (all powers of the number \(2\)), and in the set some of the weights might be the same. Weights were placed on two cups of the scales so that the scales are in balance. It is known that on the left cup, all weights are different. Prove that there are as many weights on the right cup as there are on the left.

\(CD\) is a chord of a circle with centre \(A\). The line \(CD\) is parallel to the tangent to the circle at the point \(B\). Prove that the triangle \(BCD\) is isosceles.

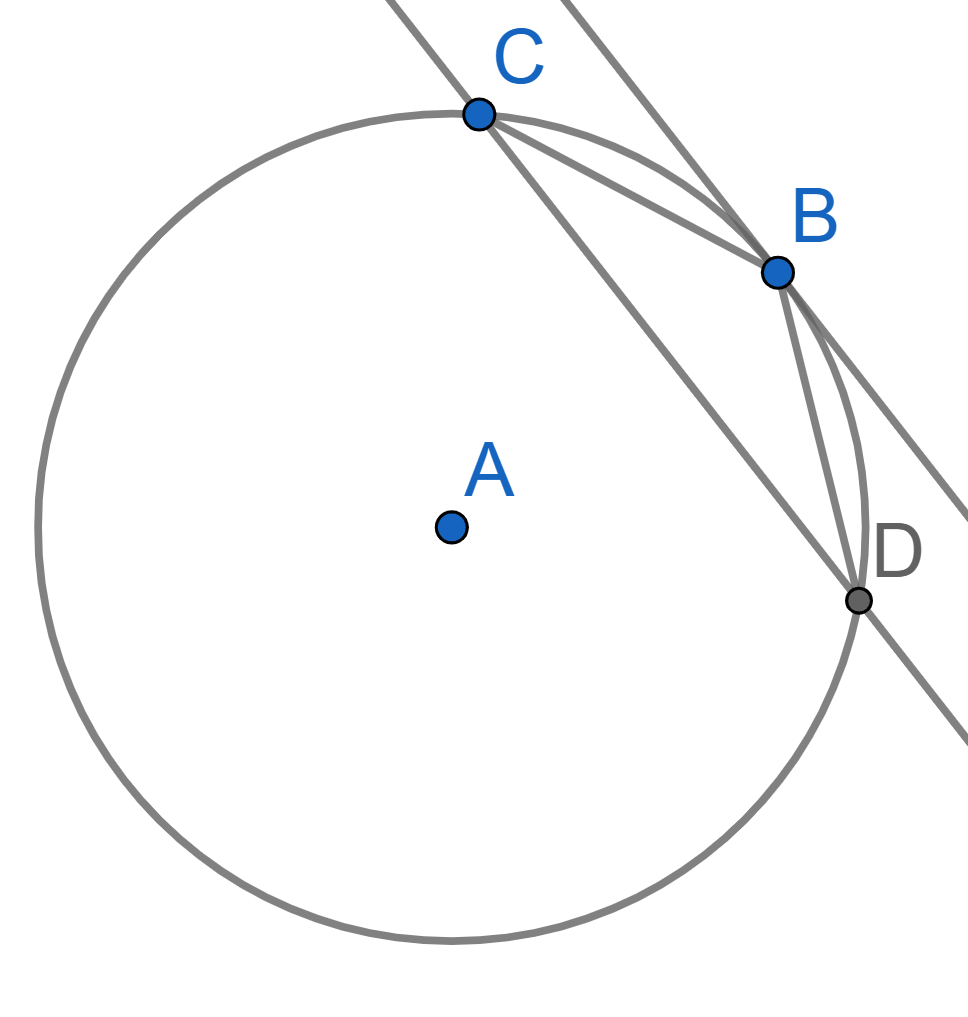
Four lines, intersecting at the point \(D\), are tangent to two circles with a common center \(A\) at the points \(C,F\) and \(B,E\). Prove that there exists a circle passing through all the points \(A,B,C,D,E,F\).

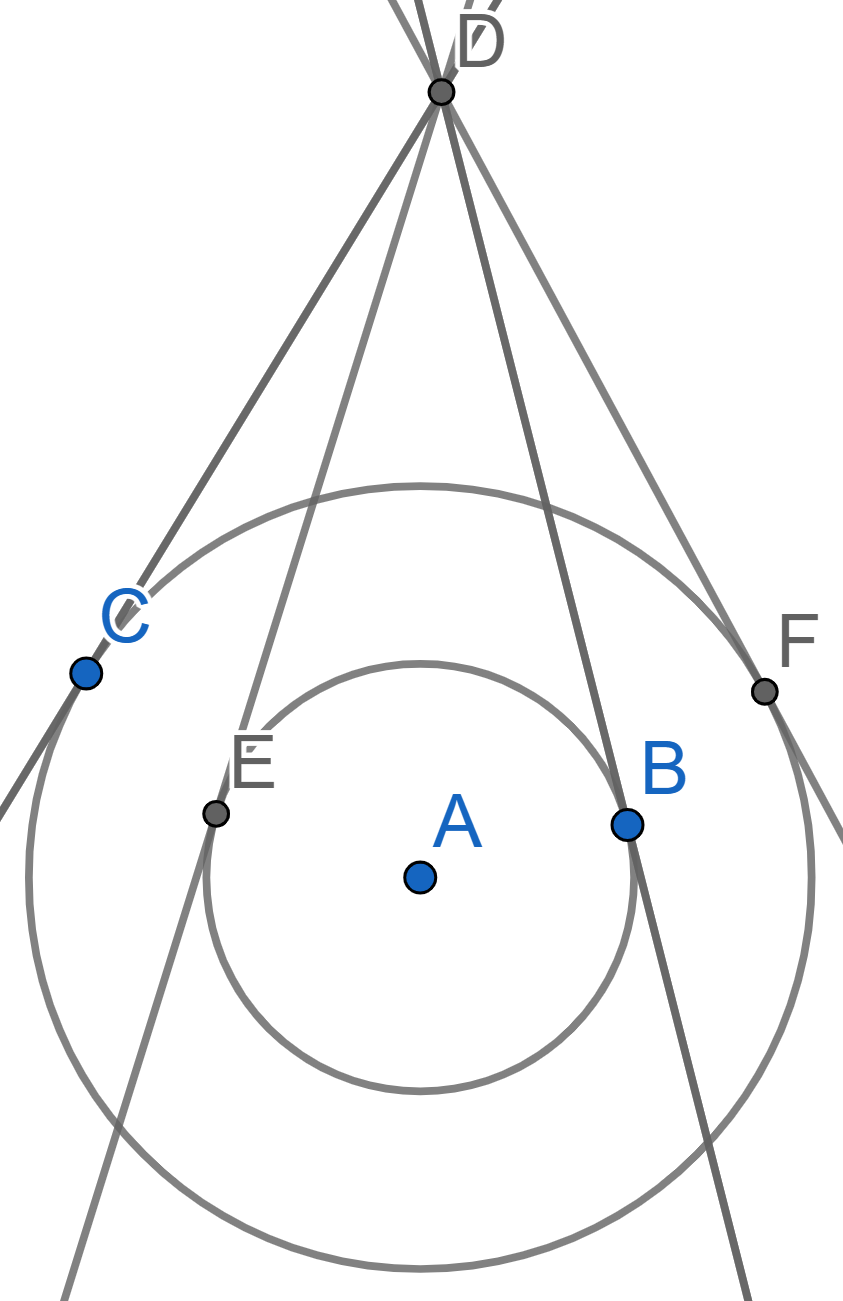
A circle with center \(A\) is inscribed into the triangle \(CDE\), so that all the sides of the triangle are tangent to the circle. We know the lengths of the segments \(ED=c, CD=a, EC=b\). The line \(CD\) is tangent to the circle at the point \(B\) - find the lengths of segments \(BD\) and \(BC\).

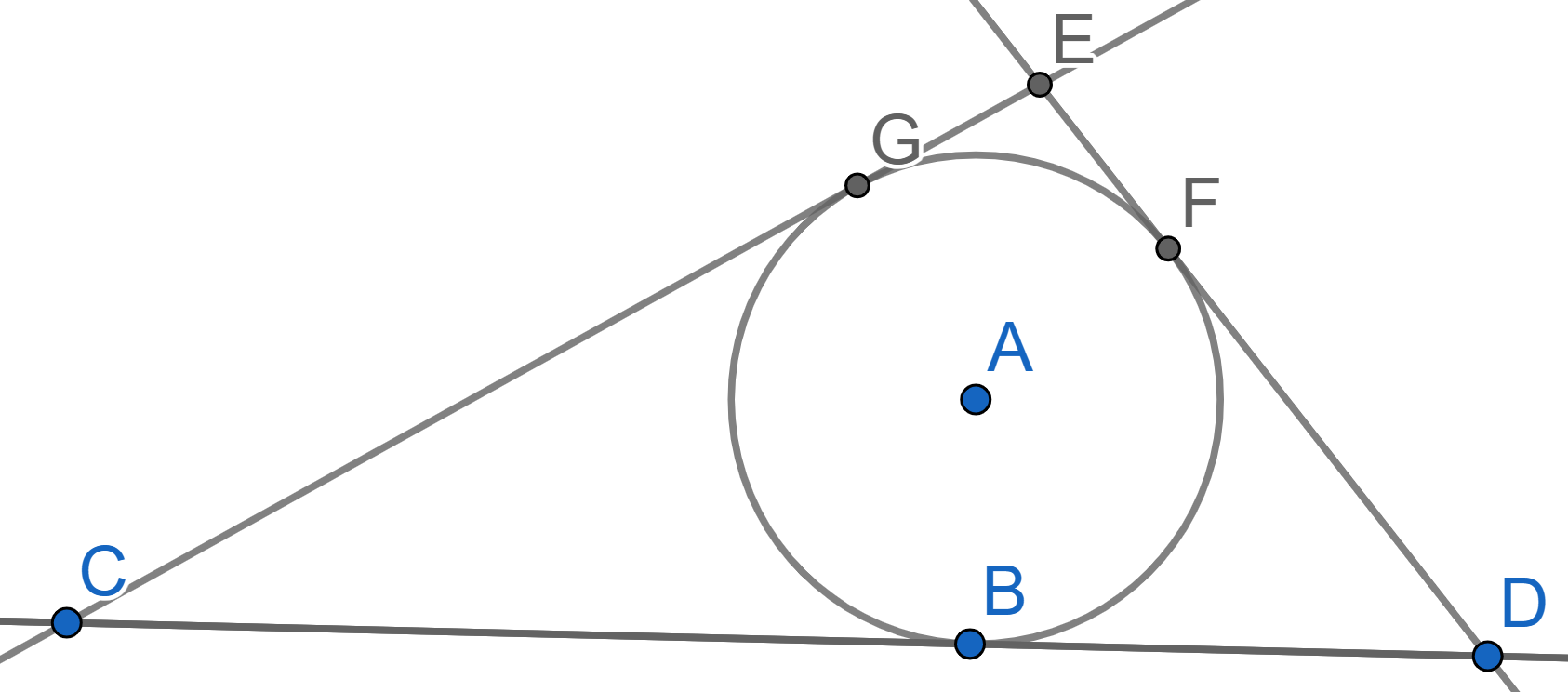
A circle with center \(A\) is tangent to all the sides of the quadrilateral \(FGHI\) at the points \(B,C,D,E\). Prove that \(FG+HI = GH+FI\).

Is it true that if \(a\) is a positive number, then \(a^2 \ge a\)? What about \(a^2 +1 \ge a\)?

The numbers \(a\), \(b\) and \(c\) are positive. By completing the square, show that \[\frac{a^2}4 + b^2 + c^2 \ge ab-ac+2bc.\]

Let \(m\) and \(n\) be natural numbers such that \(m>n\). Show that: \[\frac1{n^2} + \frac1{(n+1)^2} + \frac1{(n+2)^2} + \dots + \frac1{m^2} > \frac1{n} - \frac1{m}.\]